导数的本质是微小变化量,df相对于dx的变化率
df / dx ,x 每单位的变化引起的函数变化率,df是f(x)变化的值,dx是x变化的值
dx是一个非常微小的值,对于非常微小的值,可以忽略掉任何包含多于一个dx的项
df是正方形多出来的面积,2*dx*x + dx^2,dx^2可以忽略,所以x^2的导数是 df/dx =2x
*****
幂函数x^n的导数是n*x^n-1
*****
(x+dx)^n的多项式展开

所以x^n导数是(x+dx)^n - x^n / dx =nx^n-1
**正弦**
正弦sine,数学术语,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
*****
**余弦**
余弦(余弦函数),三角函数的一种。在Rt△ABC(直角三角形)中,∠C=90°(如图所示),∠A的余弦是它的邻边比三角形的斜边,即cosA=b/c,也可写为cosa=AC/AB。余弦函数:f(x)=cosx(x∈R)。
临边比斜边
sinθ的导数是cosθ
*****
# 复合函数求导
函数相加 函数相乘 嵌套的函数

**一**
两个函数的和的导数等于两个函数的导数的和

*****
数学当中的乘积运算通过几何面积来理解最好



*****
d(x^2)表示 函数x^2的变化,函数某点附近的变化率就是该点附近的导数。
时长回想公式的意义
df/dx 表示函数f(x)在x处的变化率,也就是导数。

数学会通过中间变量来求解
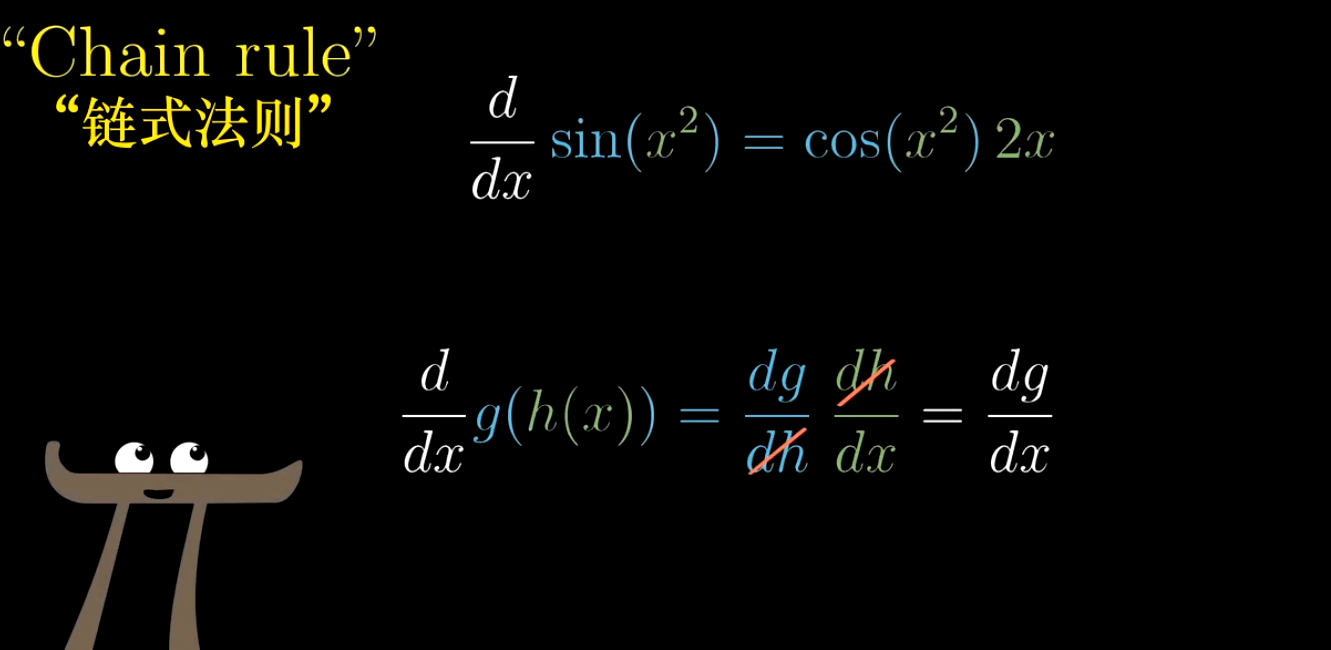
*****
