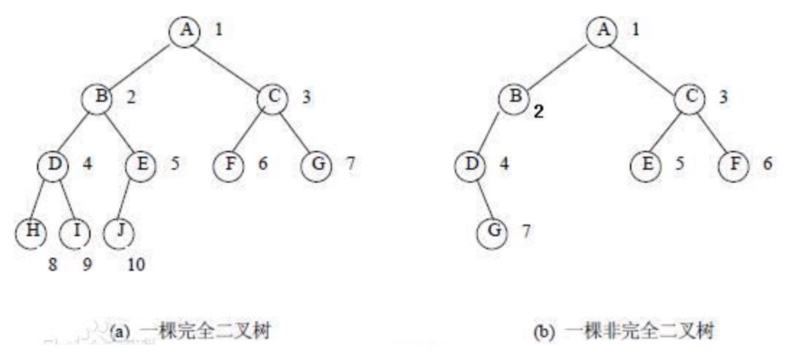
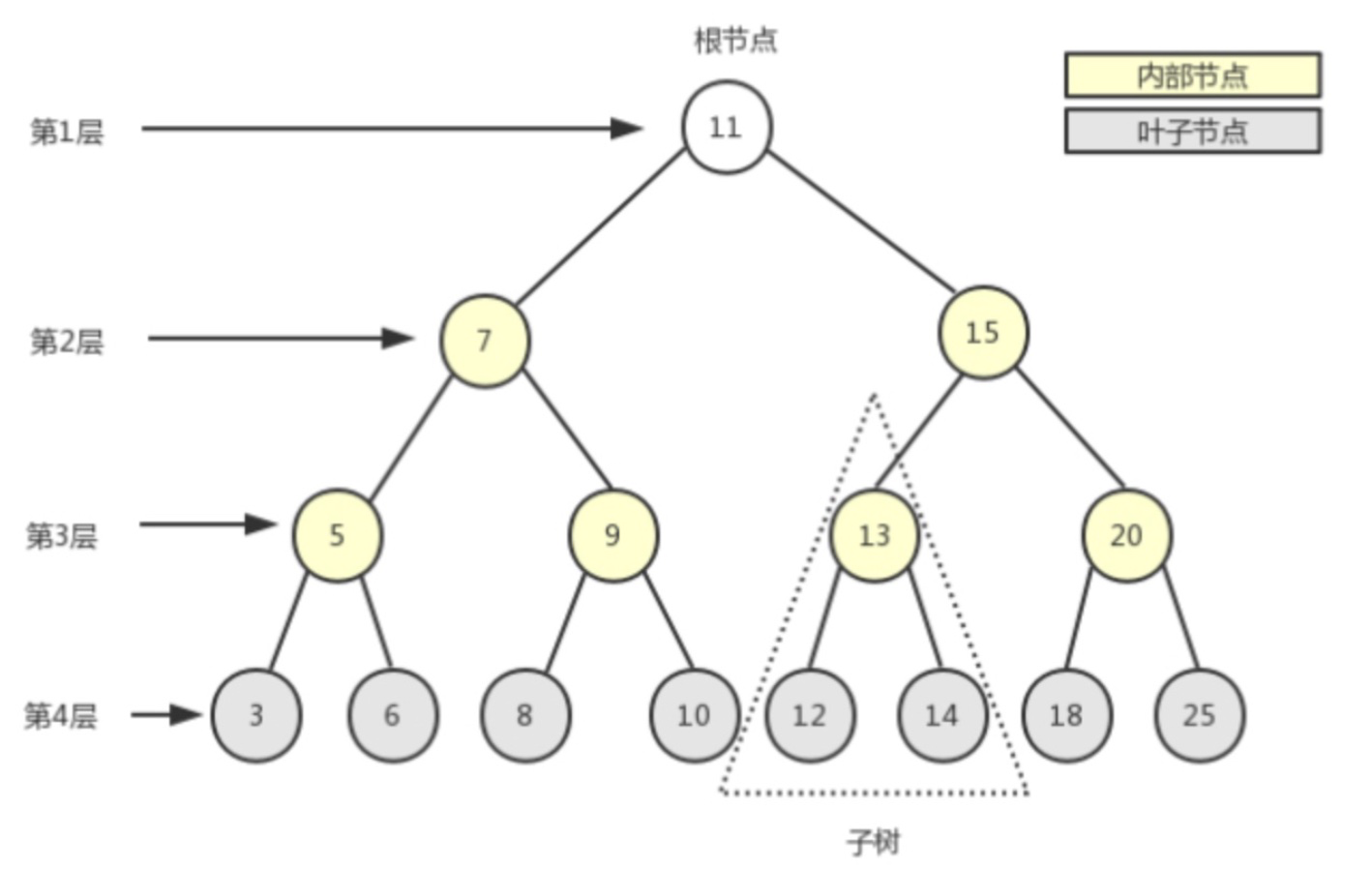
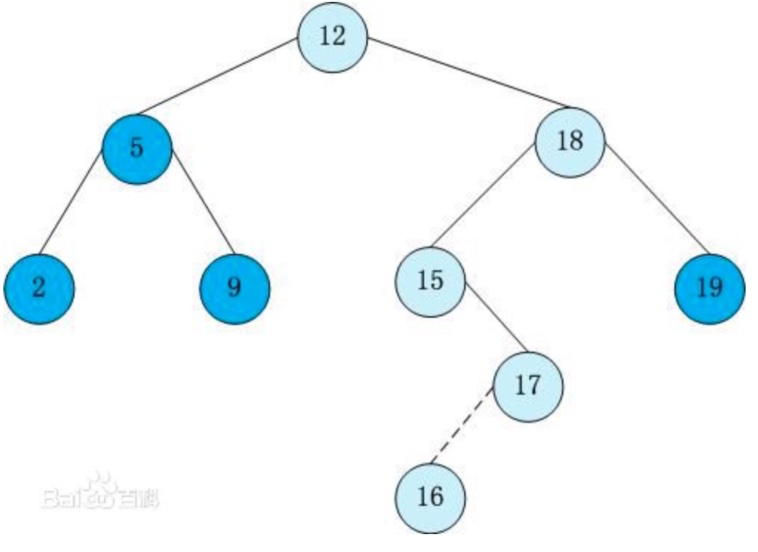
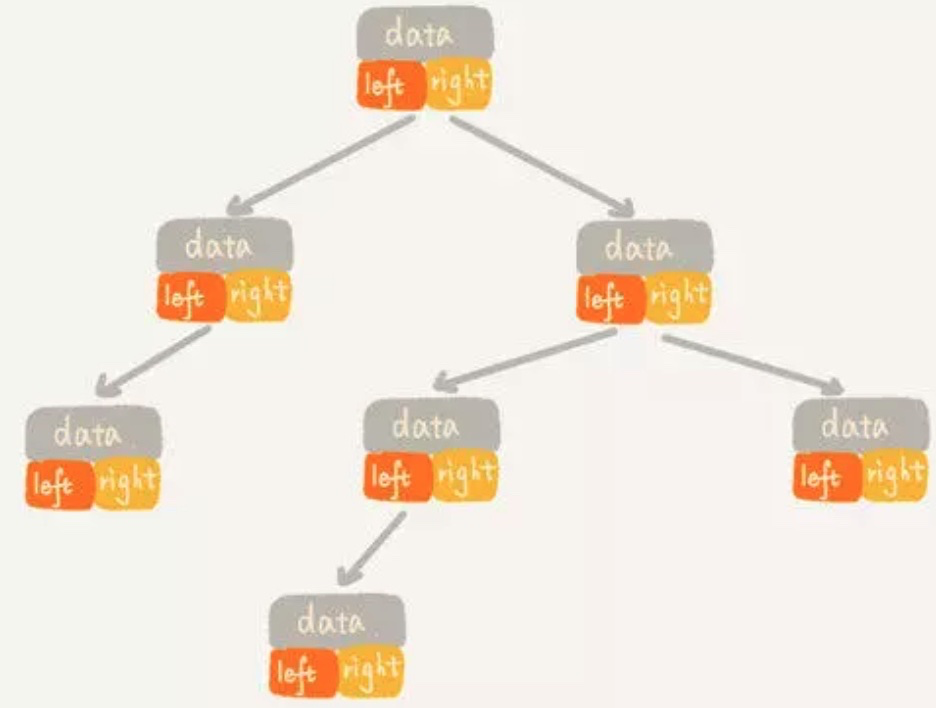
# 介绍 ## 特点 二叉树： `最多只有两个` 子节点的树。度为2的数。  ## 分类 二叉树分为： - 满二叉树 - 完全二叉树 - 平衡二叉树 - 二叉搜索树 ### 满二叉树 除了最后一层叶子结构之外，其他节点都有两个子节点的树。  ### 完全二叉树 除了最后缺的几个节点不考虑之外，剩下的节点和一个满二叉结构节点数完全相同。  ### 平衡二叉树 任一节点左右子节点的 `高度差` 小于等于 |1|。 节点高度：从这个节点到叶子节点最多的边数。  ### 二叉搜索树（BST-Binary Search Tree） 规则： 1. 任意一个节点的左子节点都小于这个节点 2. 任意一个节点的右子节点都大于这个节点  ## 存储方式 二叉树的存储方式： - 顺序存储（用数组） - 链式存储（用链表） ### 链式存储 每个节点都有 左、右 两个指针，指向左右两个子节点。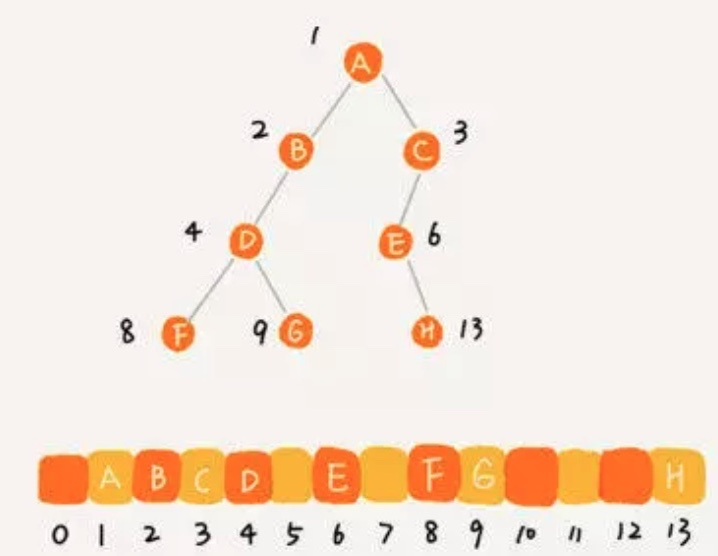  节点类： ~~~ class Node { construct(data) { this.data = data // 数据 this.left = null // 左子节点 this.right = null // 右子节点 } } ~~~ ### 顺序存储 使用数组存储二叉树。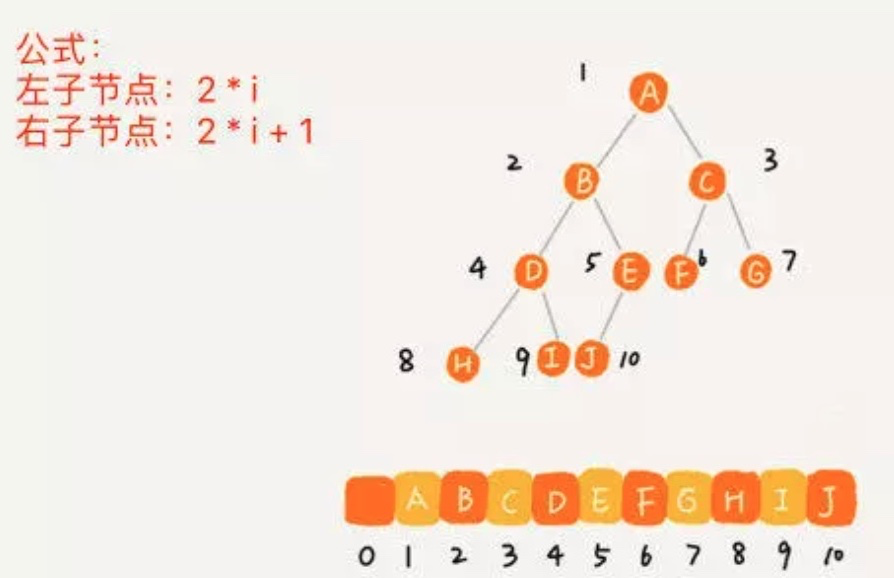 存储完之后必须要满公式： 情况一、（如果根节点保存在 0 这个下标时的公式） 第i个节点的左子节点下标：2i+1 第i个节点的右子节点下标：2i+2 第i个节点的父节点下标；Math.floor((i-1)/2) 情况二、根节点保存在1这个位置时：  顺序存储比较适合 `完全二叉树`，否则会比较浪费空间（有很多空位）：