[toc]
# 几个概念
## 路径
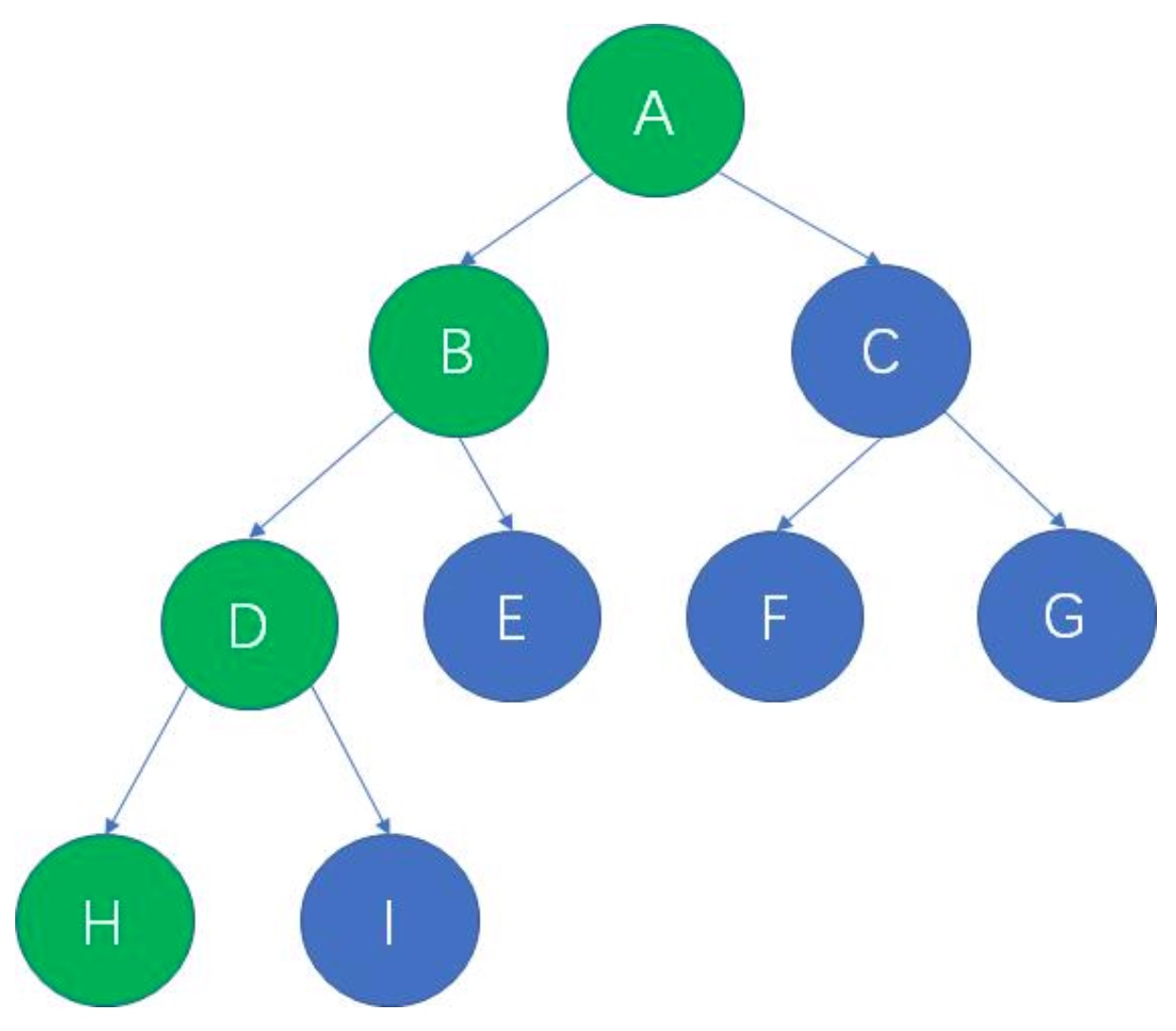
在一棵树中,从一个结点到另一个结点所经过的所有结点,被我们称为两个结点之间的路径。
比如:A -> H 的路径:
## 路径长度
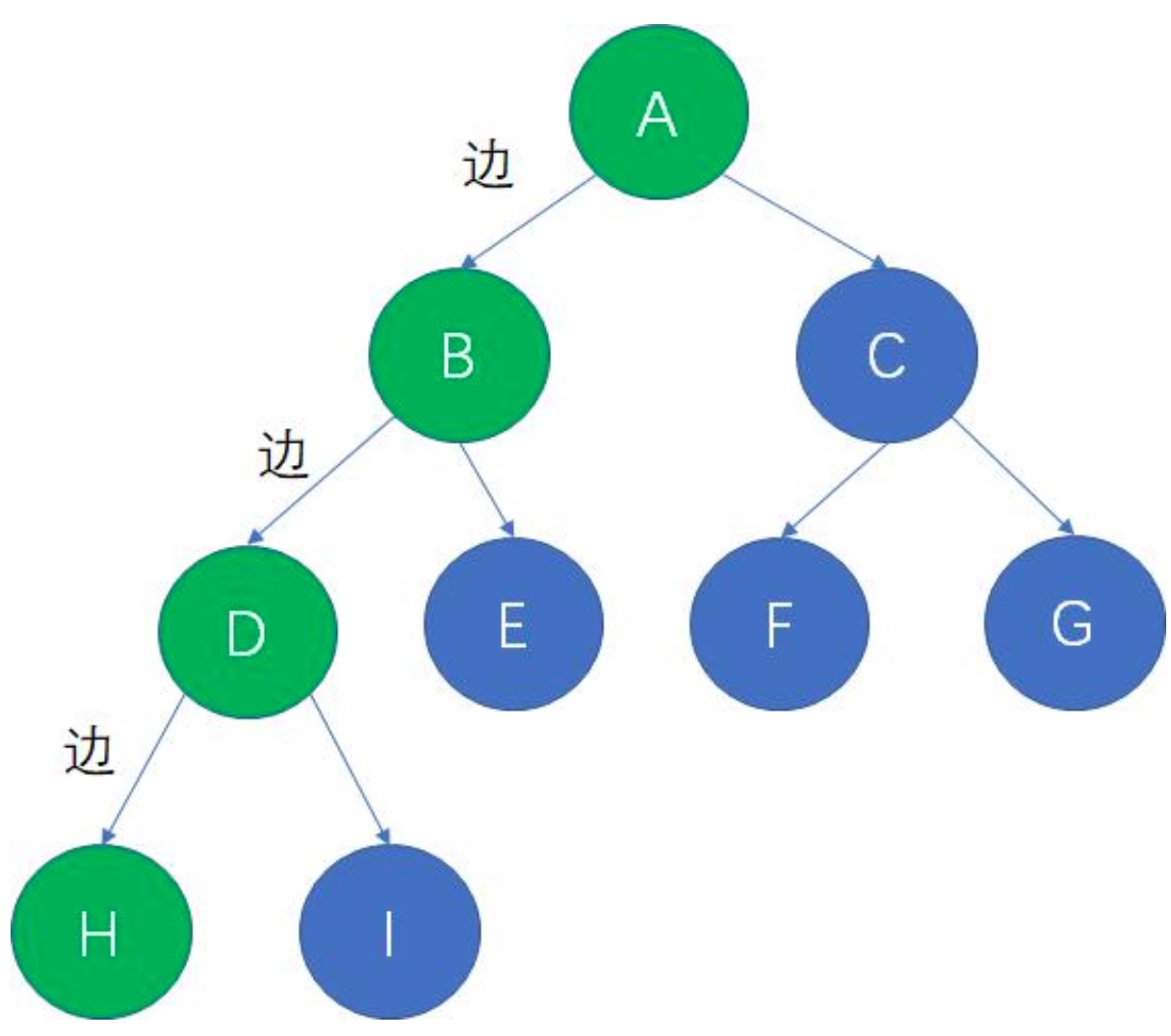
在一棵树中,从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度。
比如:A -> H的路径长度为 3:
## 节点的带权路径长度
每一个节点都可以有一个权重(数字)。
带权路径长度:节点权重 * 节点到根节点的路径长度
比如:H 的带权路径长度 = 3 * 3 = 9

## 树的带权路径长度
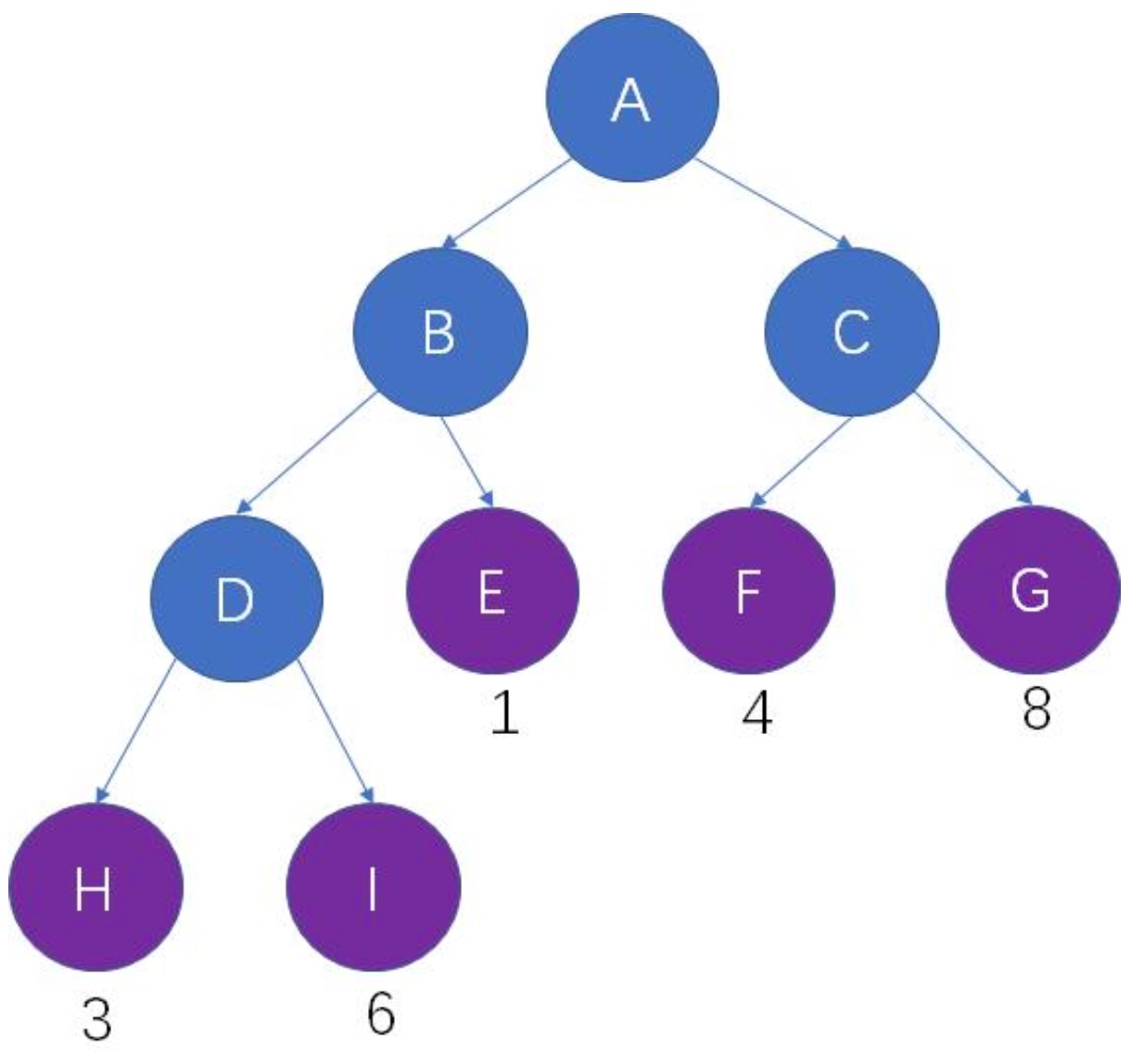
树的带权路径长度(也做WPL):所有 `叶子` 节点的带权路径长度之和。
比如:下面这棵树的 WPL = 3*3 + 6*3 + 1*2 + 4*2 + 8*2 = 53
## 哈夫曼树
哈夫曼树(Huffman Tree):是在叶子结点和权重确定的情况下,带权路径长度最小的二叉树,也被称为最优二叉树。
比如下图左侧就比右侧 WPL 小。
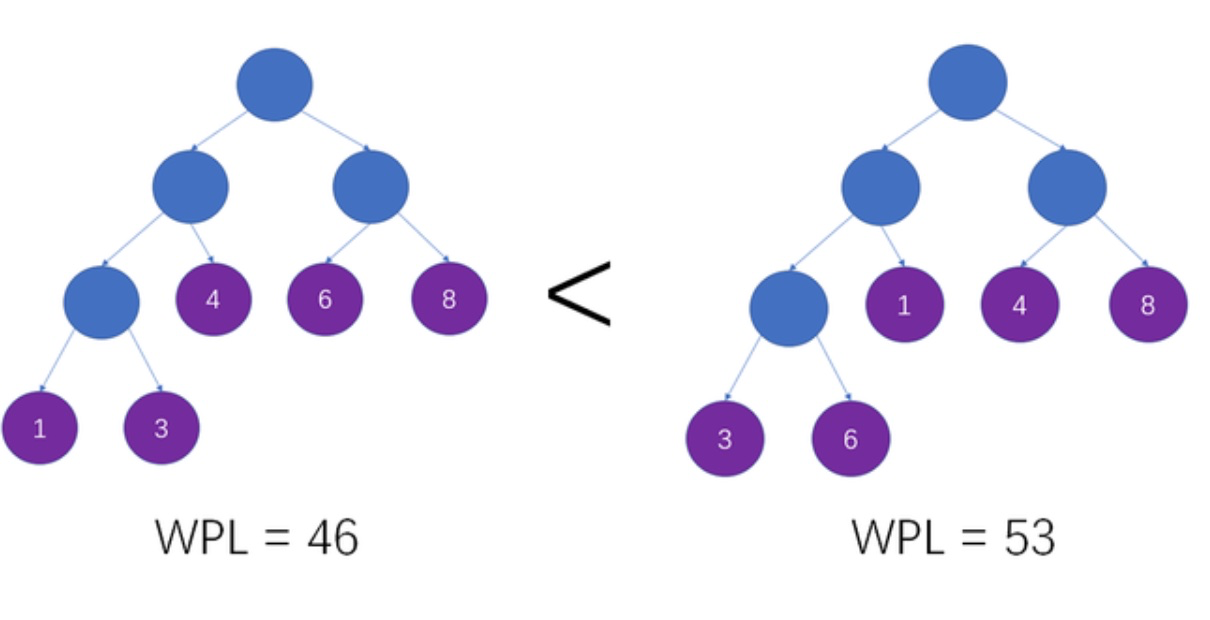
总结:核心特点:权重越大的节点,越靠近根节点。
面试官问:什么是最优二叉树?什么是哈夫曼树?
## 哈夫曼编码
哈夫曼编码可以用来进行 `数据压缩` 。
### 编码
比如要压缩:“acbcbacddaddaddccd”
1. 先统计文本中每个字符出现的频率
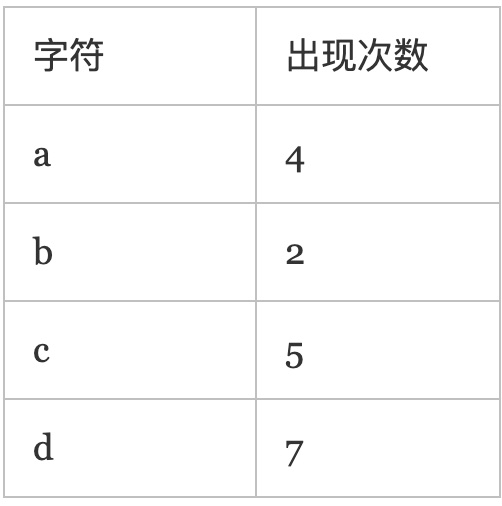
2. 频率当作权重构建哈夫曼树

3. 根据哈夫曼树对字符串进行编码
编码规则:
1. 左子节点是0,右子节点是1
2. 从根节点到叶子结果
根据哈夫曼树可以将字符串编码为:
* a:111
* ac:1111 0
* acb:1111 0110
* acbc:1111 011010
* acbcb:1111 0110 1011 0…
说明:编码之后好像是变长了,但注意这里的存储 单位是不同的:
- 1 字节(Byte) = 6 位(bit)
- 一个字母 = 1 字节 = 8 位
- 一个汉字 = 2~4字节 = 16~32位
- 而1010这个哈夫曼编码,单位是位,一个1或0只带1 位。
所以综合:哈夫曼编码的压缩率在 20% ~ 90% 之间。
### 解码
编码过程就是:
1. 将哈夫曼编码到哈夫曼树上 “从根向下跑一遍”
2. 0 向左、 1 向右
3. 当遇到一个 “叶子” 节点时结束
4. 重复从根开始跑,重复 1~3
比如:1111 0110 1011 0... 到树上跑得到:acbcb
## 用途
1. 数据压缩
2. 加密、解密
# 构建哈夫曼树的流程
1. 将带权节点 `按升序` 放到数组中
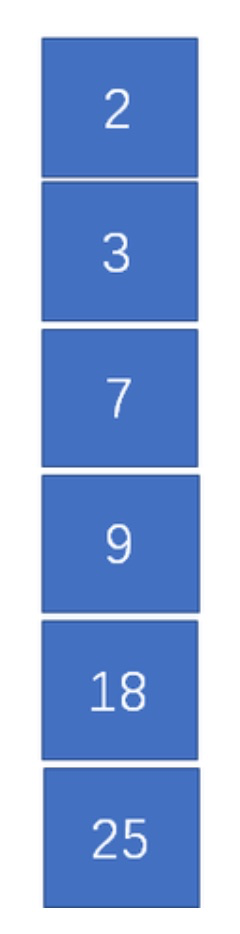
2. 取出数组中最小的两个节点做为子节点构造一棵树,和为父节点
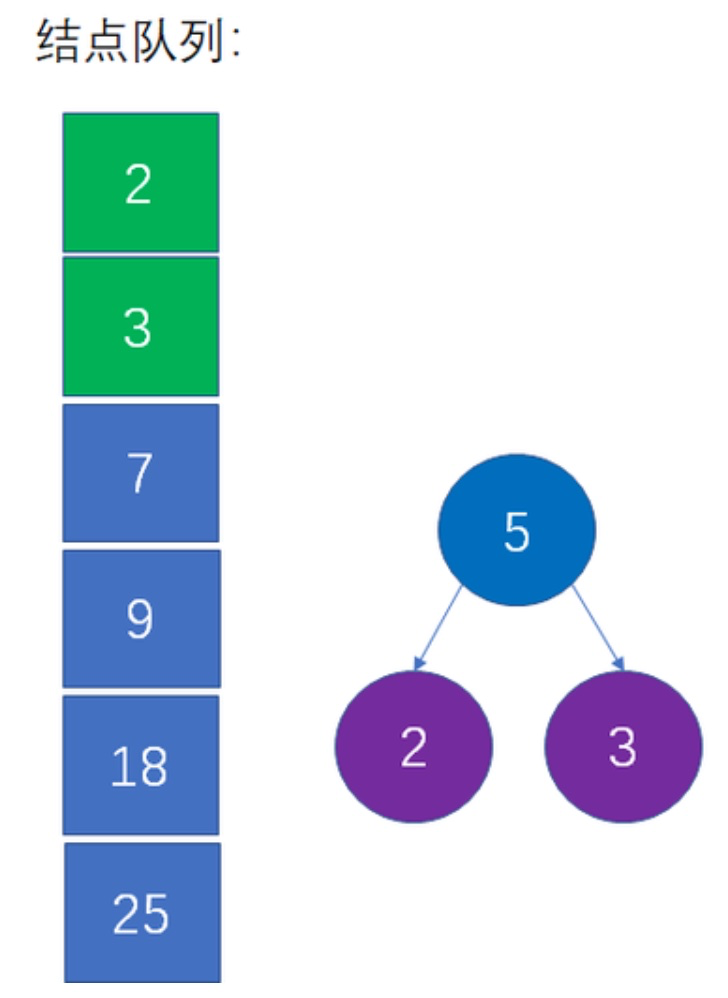
3. 将父节点的值放回数组中并 `排序`
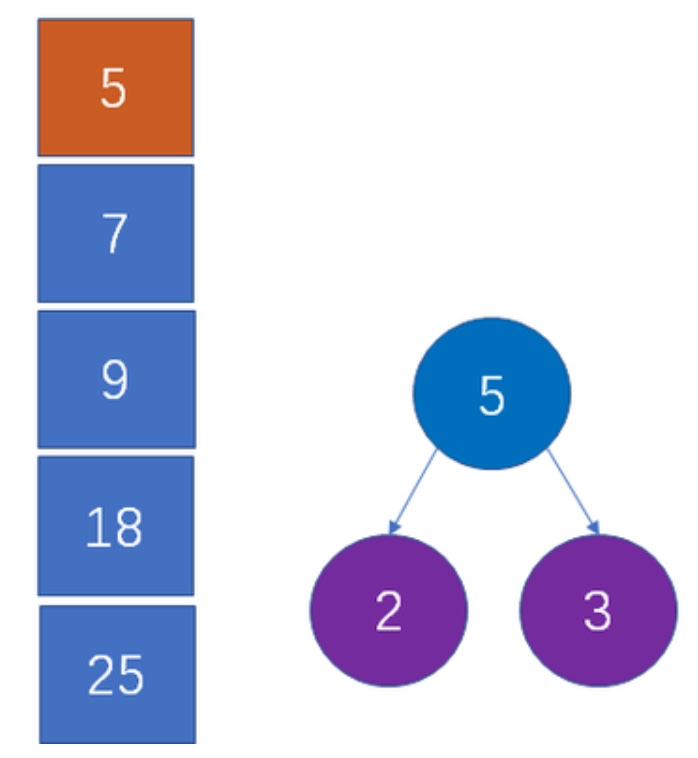
4. 重复2~3步骤
拿出最小两个节点:
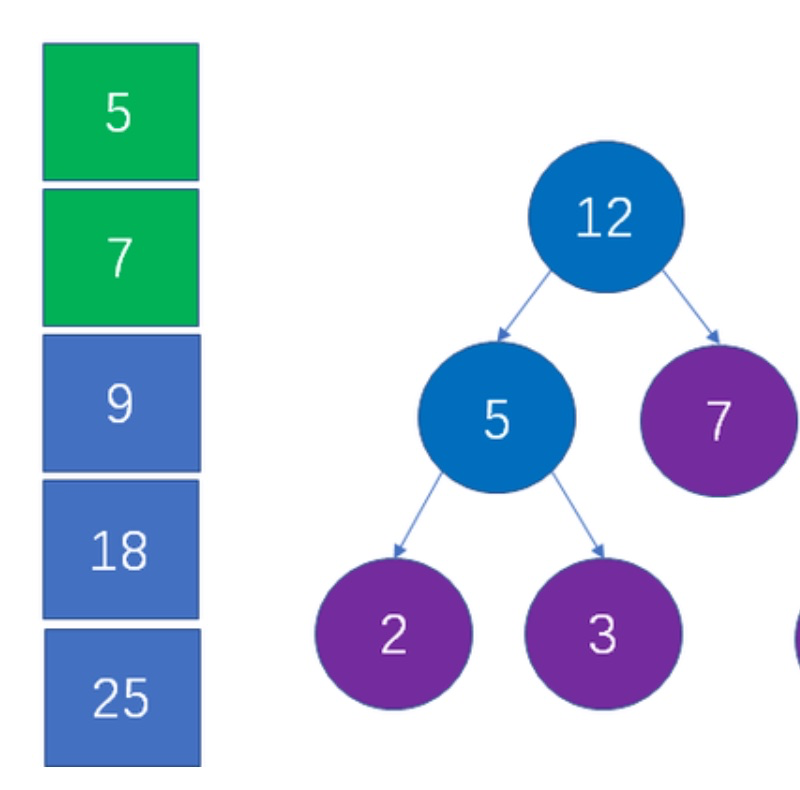
将的父节点放回并排序

5. 重复2~3
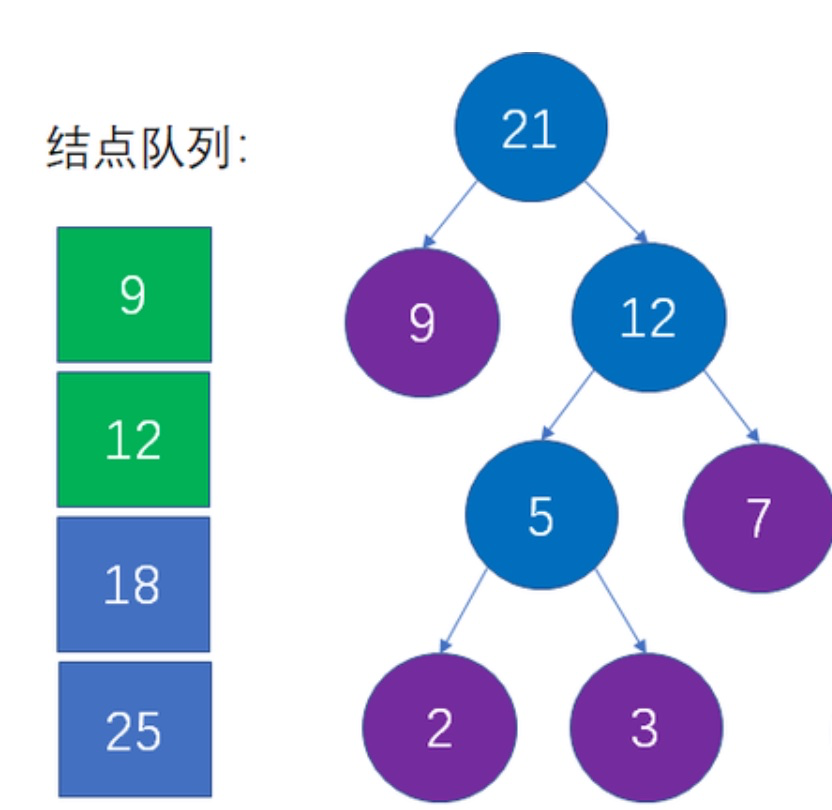
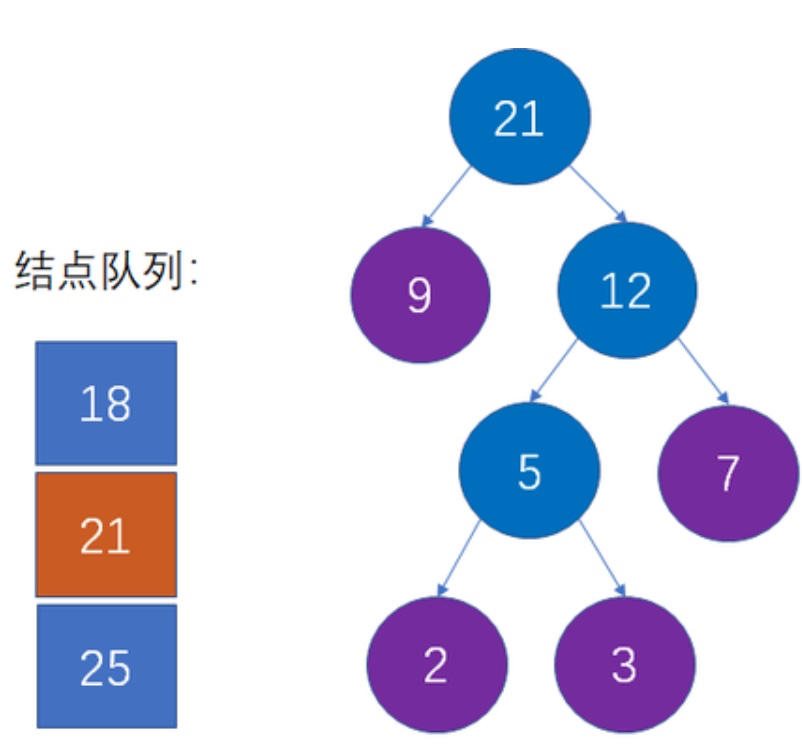
6. 重复2~3
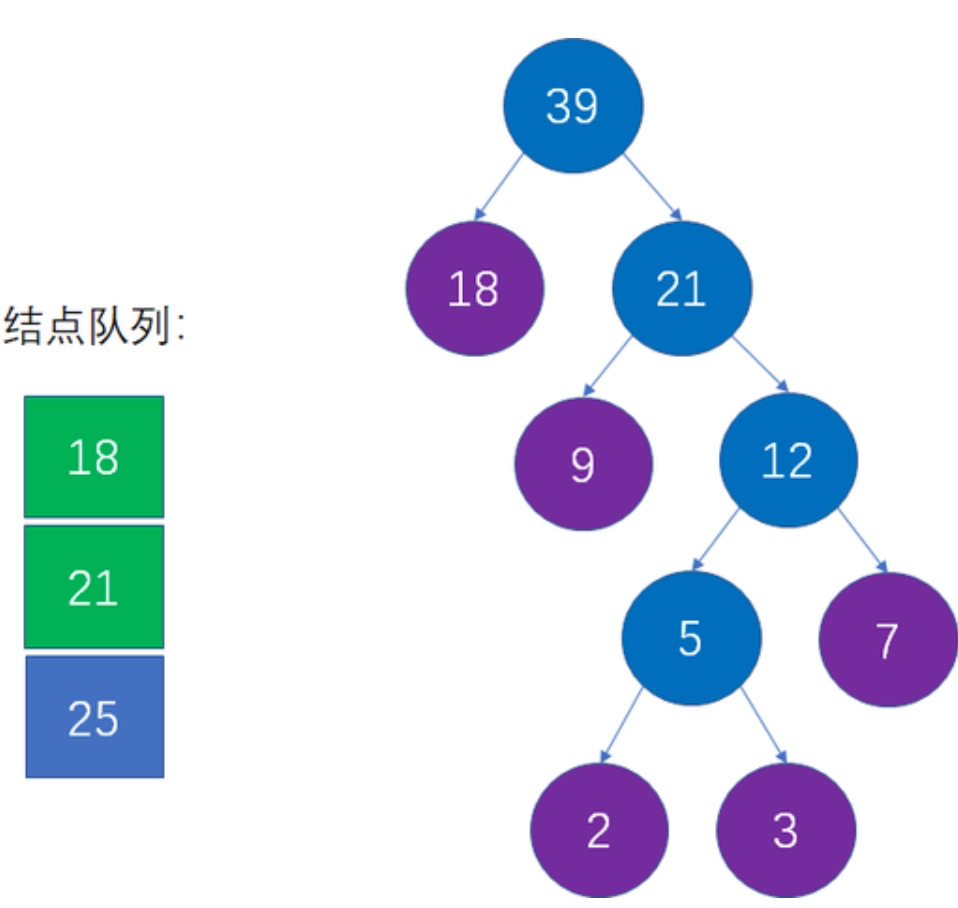

7. 重复2~3

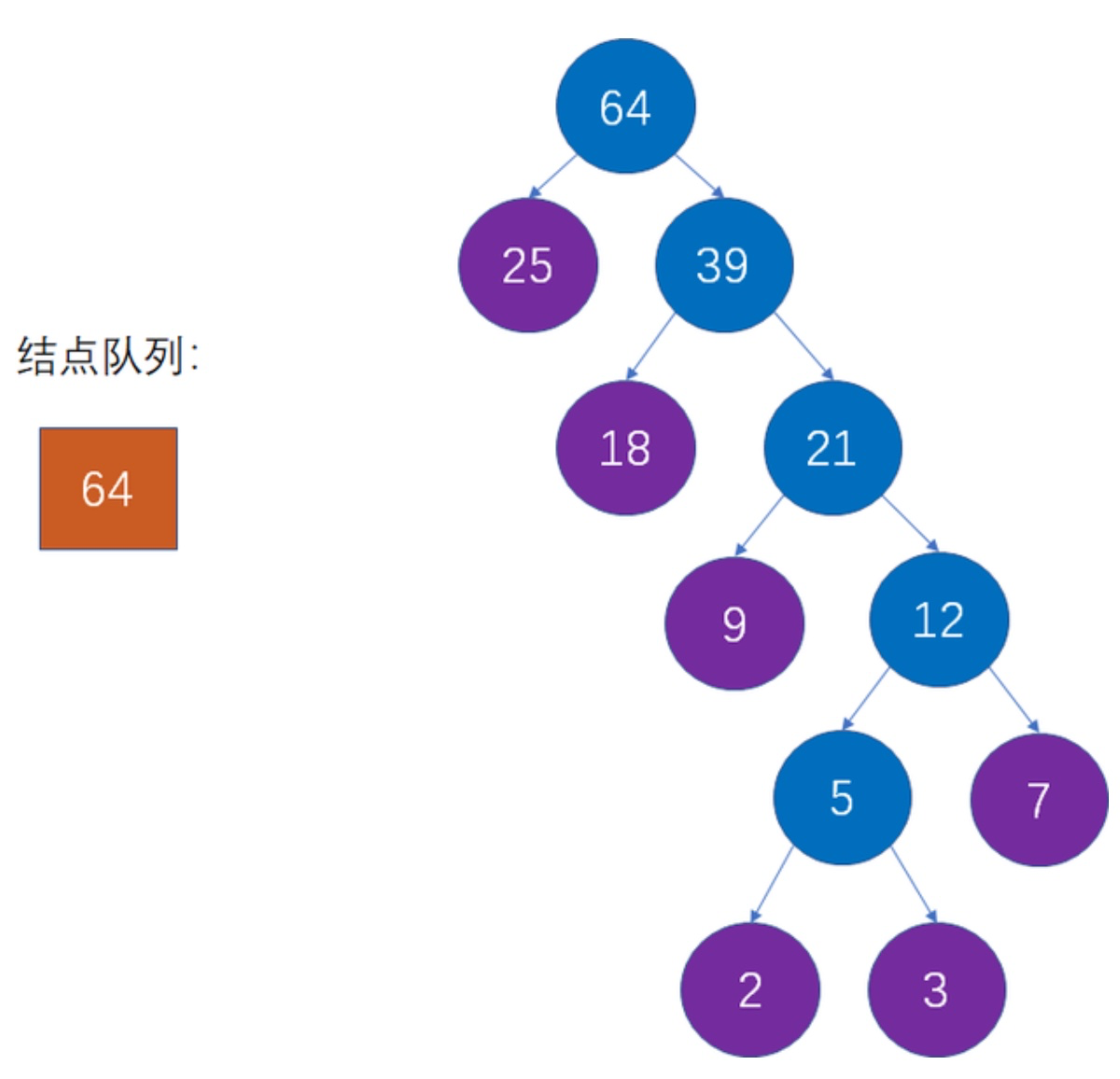
最后数组中只剩下一个节点,说明构造结束!
# 代码实现 - 构造哈夫曼树
~~~
class Node {
constructor(data) {
this.data = data
this.left = null
this.right = null
}
}
class HuffmanTree {
constructor(arr) {
this.queue = arr
this.root = null
let first, second, parent
while(this.queue.length>1) {
// 排序
this.queue.sort((a,b)=>a-b)
first = this.queue.shift()
second = this.queue.shift()
parent = first + second
this.queue.unshift(parent)
parent = new Node(parent)
first = new Node(first)
second = new Node(second)
if(this.root === null) {
parent.left = first
parent.right = second
this.root = parent
} else {
if(this.root.data == first.data) {
parent.left = this.root
parent.right = second
this.root = parent
} else {
parent.left = first
parent.right = this.root
this.root = parent
}
}
}
}
}
~~~
