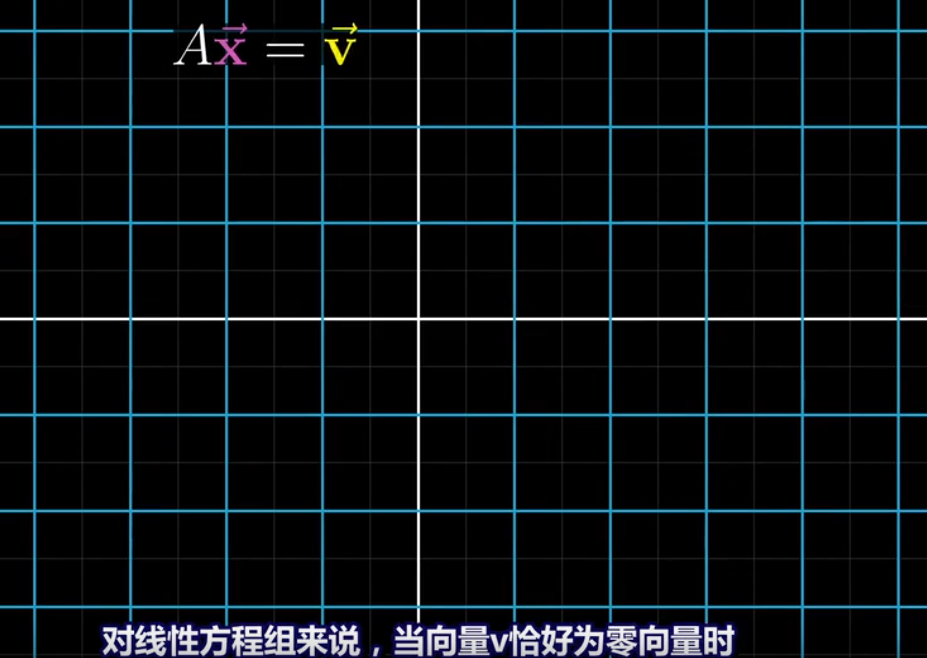
求矩阵的行列式,矩阵的行和列要相等
*****
矩阵可以用来求解线性方程组:
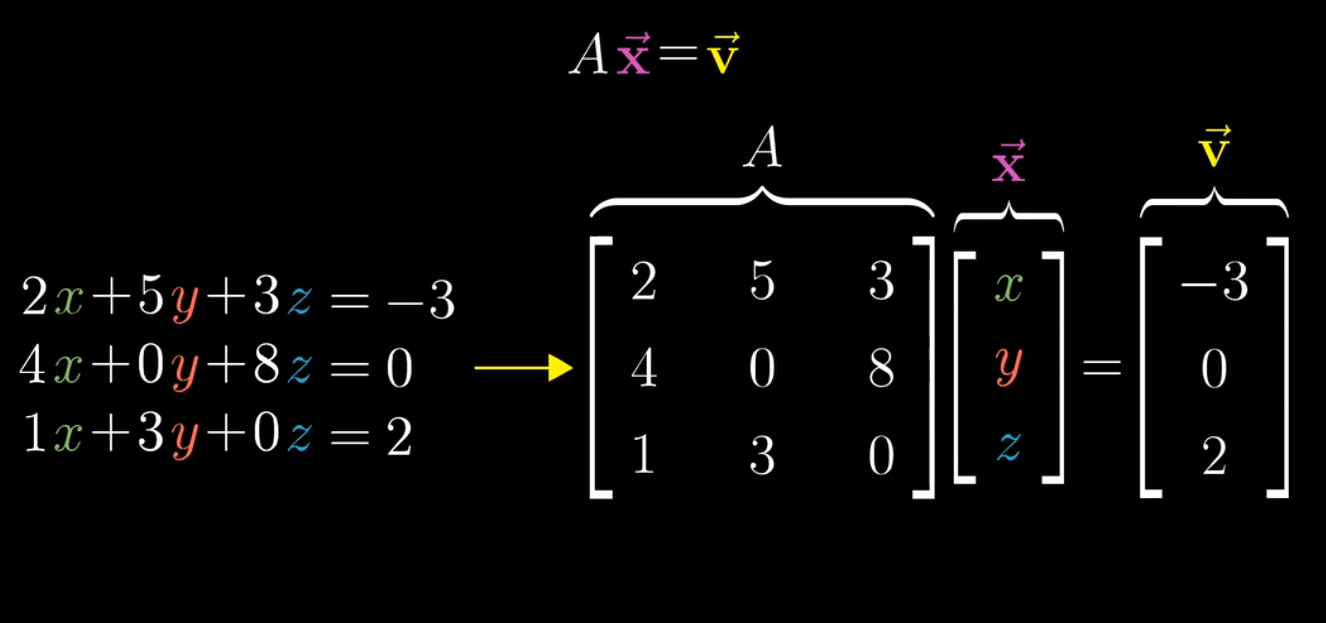
一个线性变换将向量x变为向量v
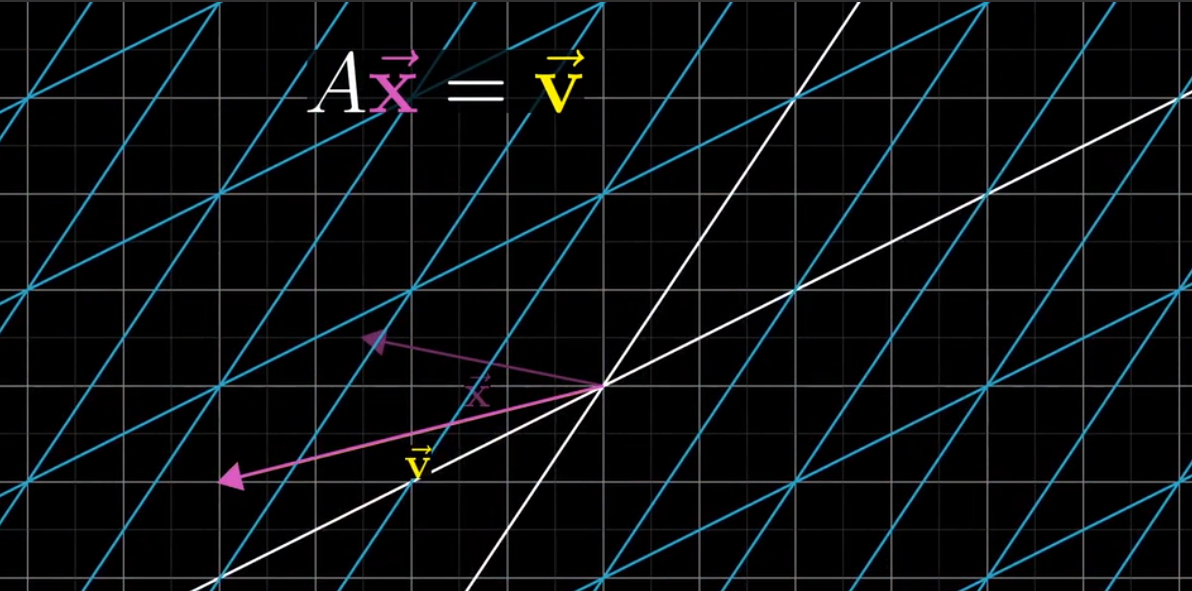
*****

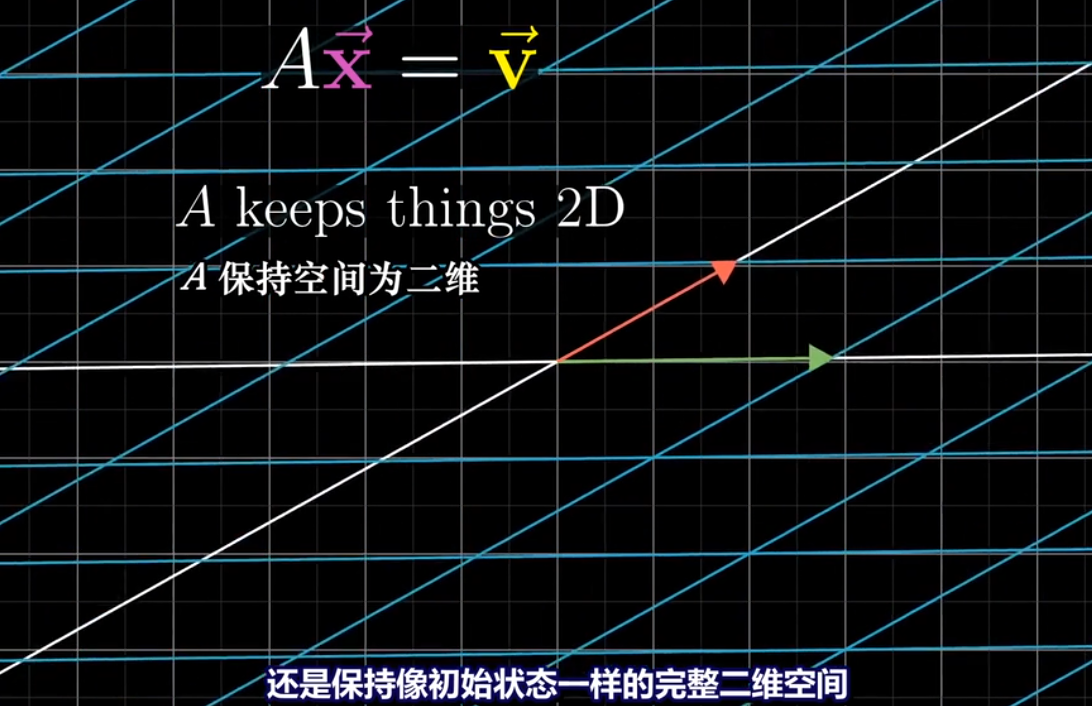
*****
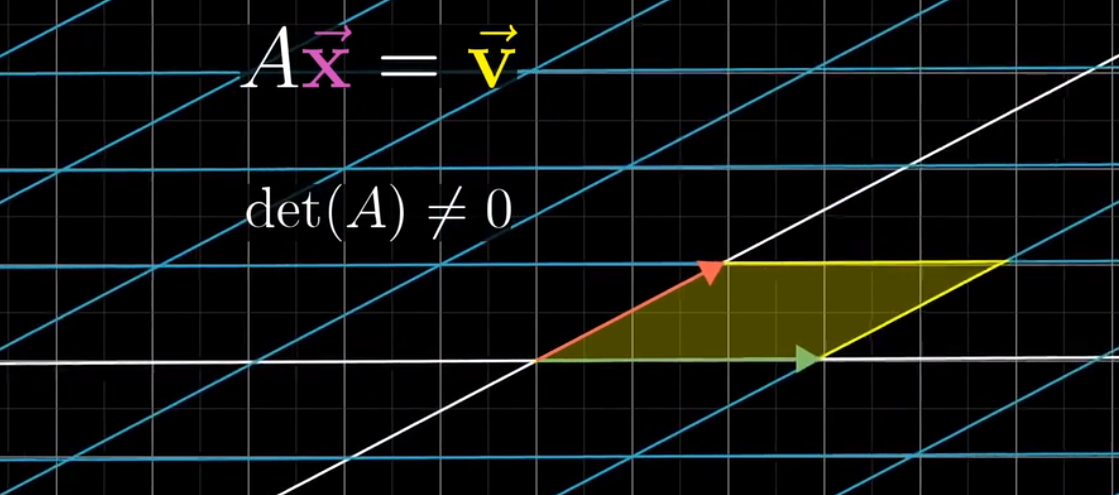
变换A的行列式不为0
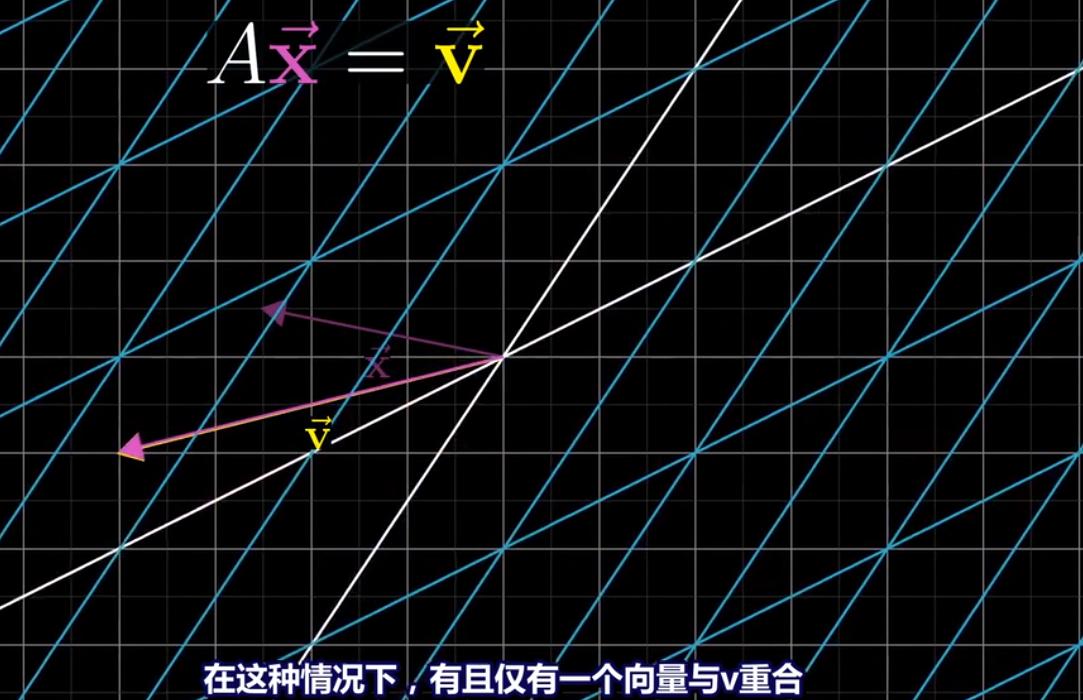
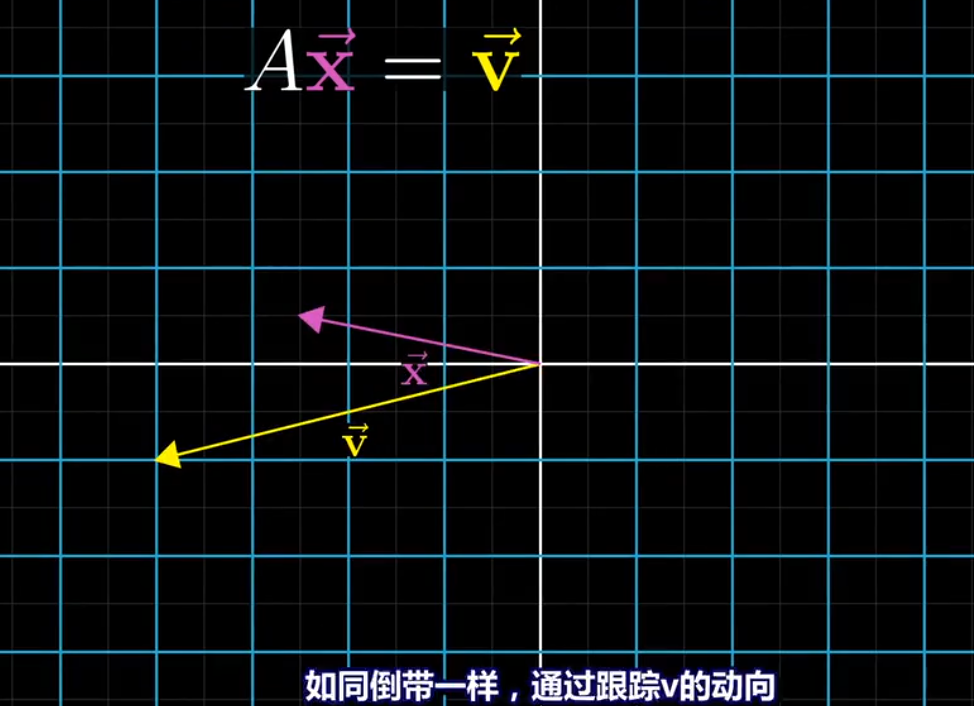
v向量通过逆变换来找到x向量
**逆变换**
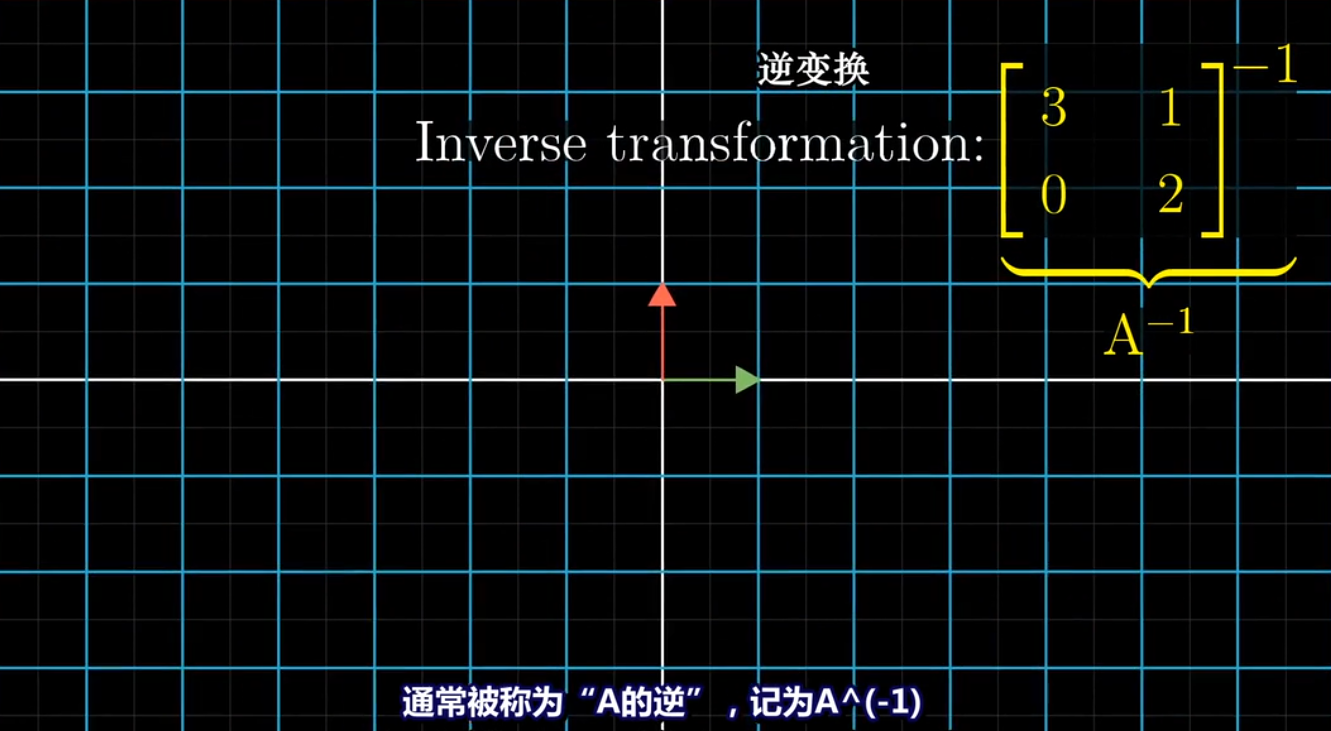
先进行线性变换A,再进行逆变换。结果为原坐标系回到初始状态,基向量**i**和**j**都保持不变

*****

在两边同时乘A的逆矩阵来求解向量X。在几何上的意义就是对向量v进行A的逆向变换来找到向量x

*****
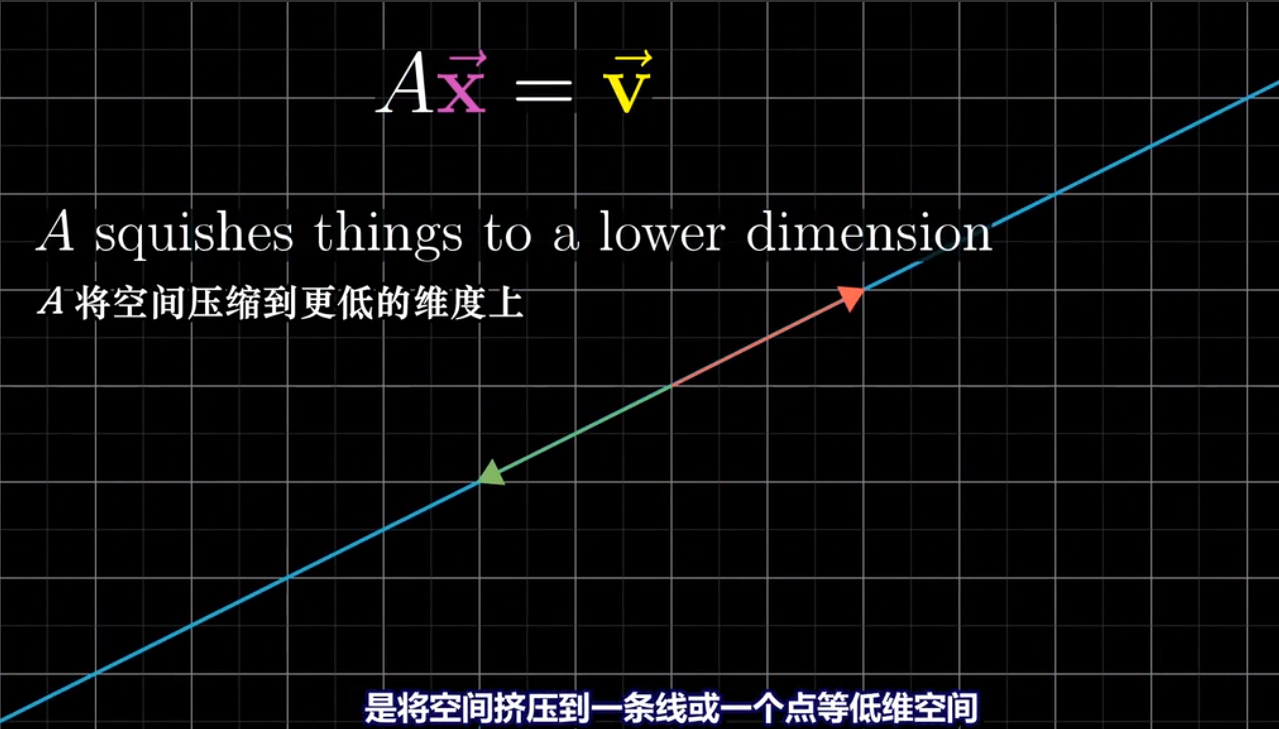
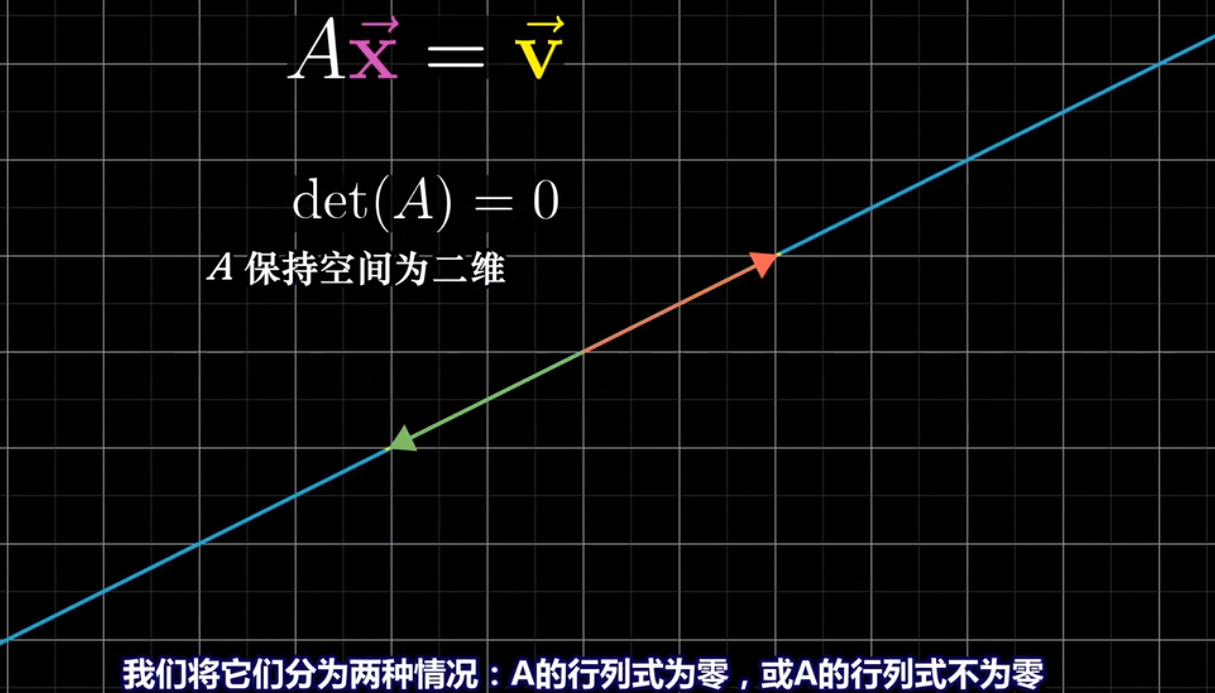
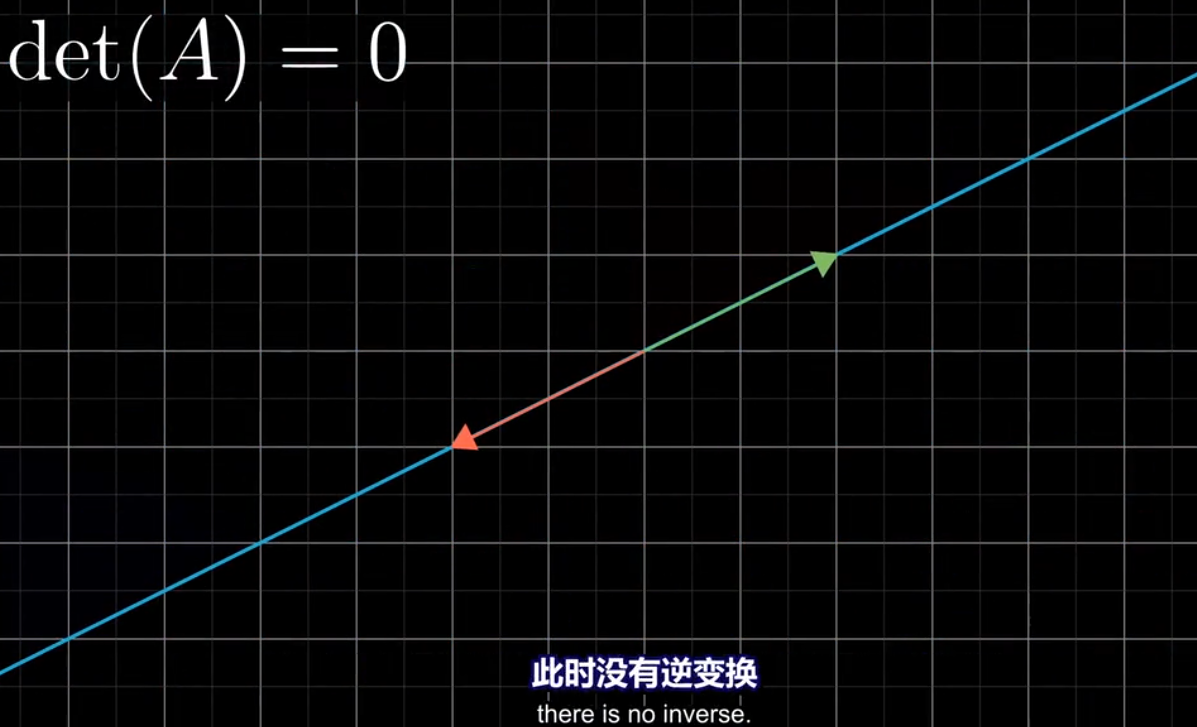
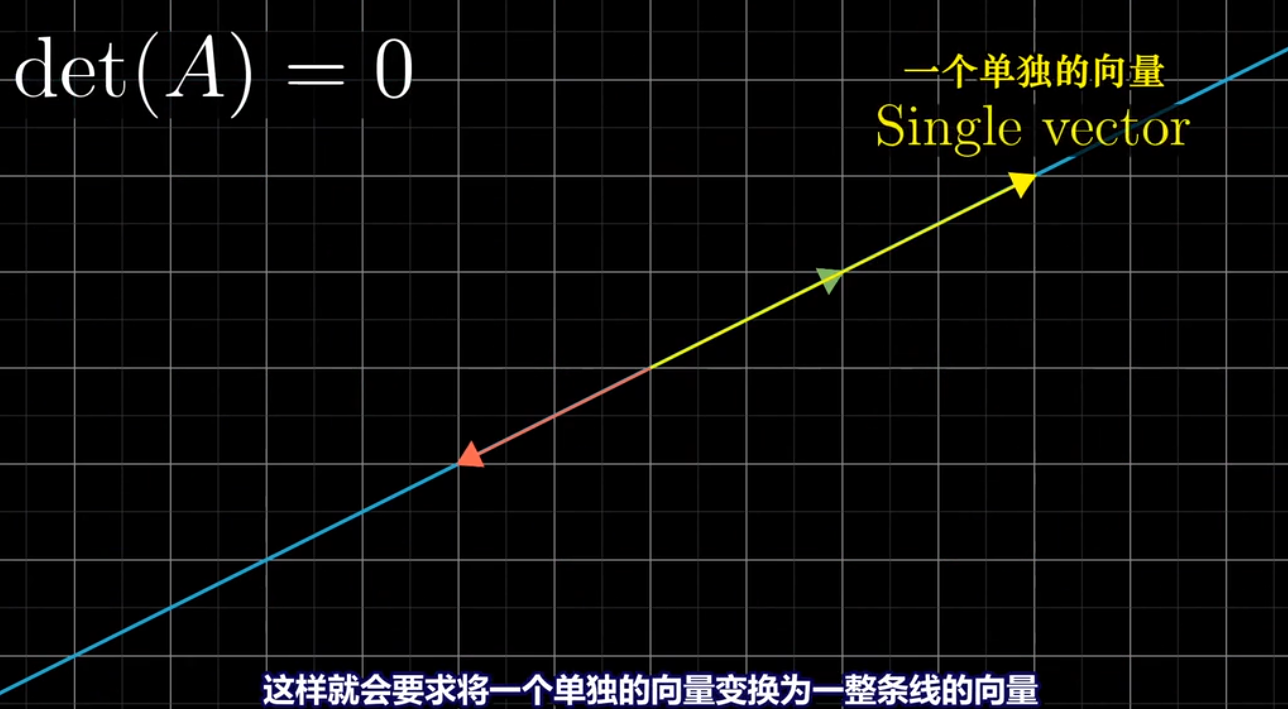
## 当行列式det(A)=0时


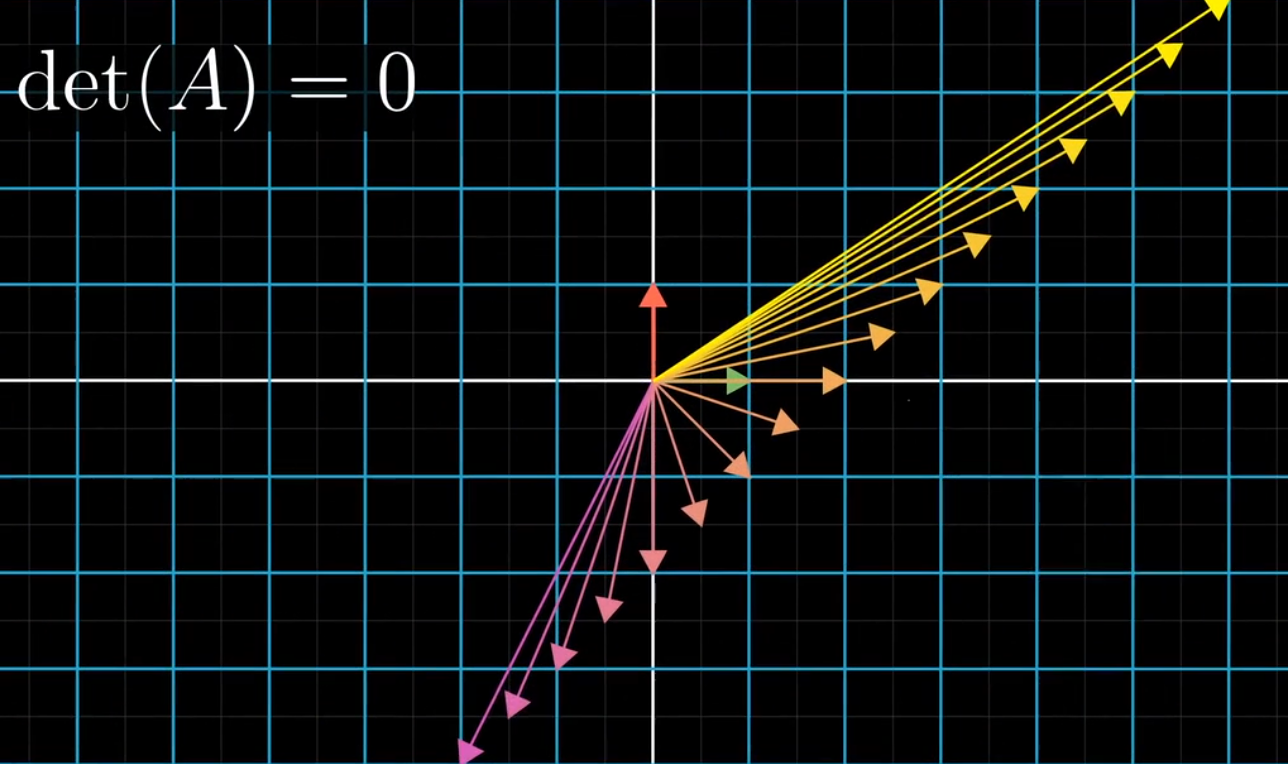
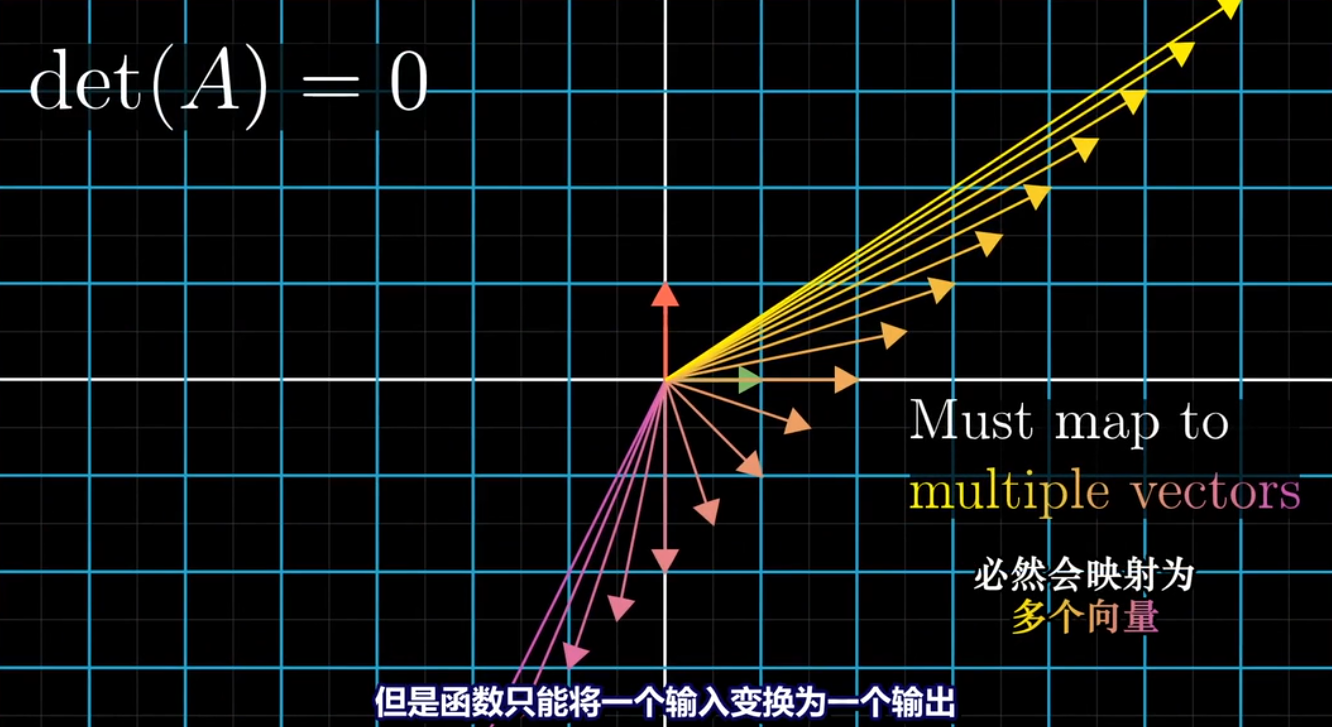
*****
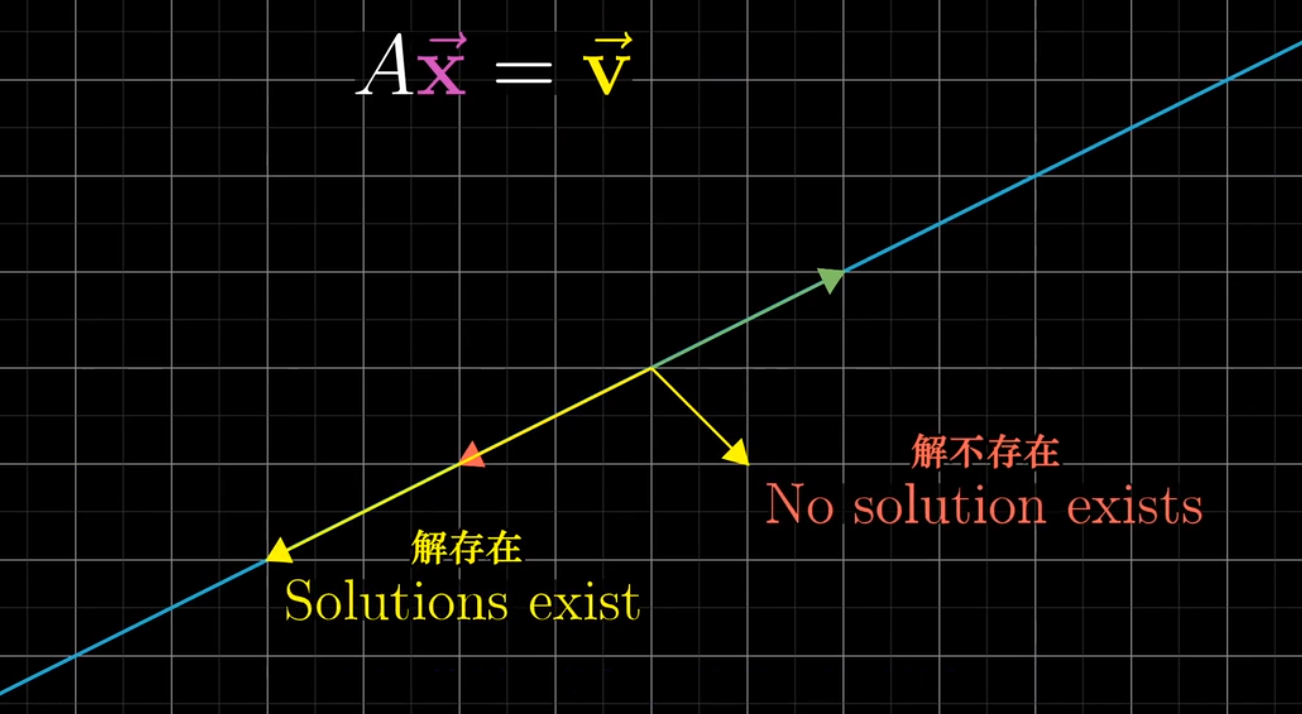
*****
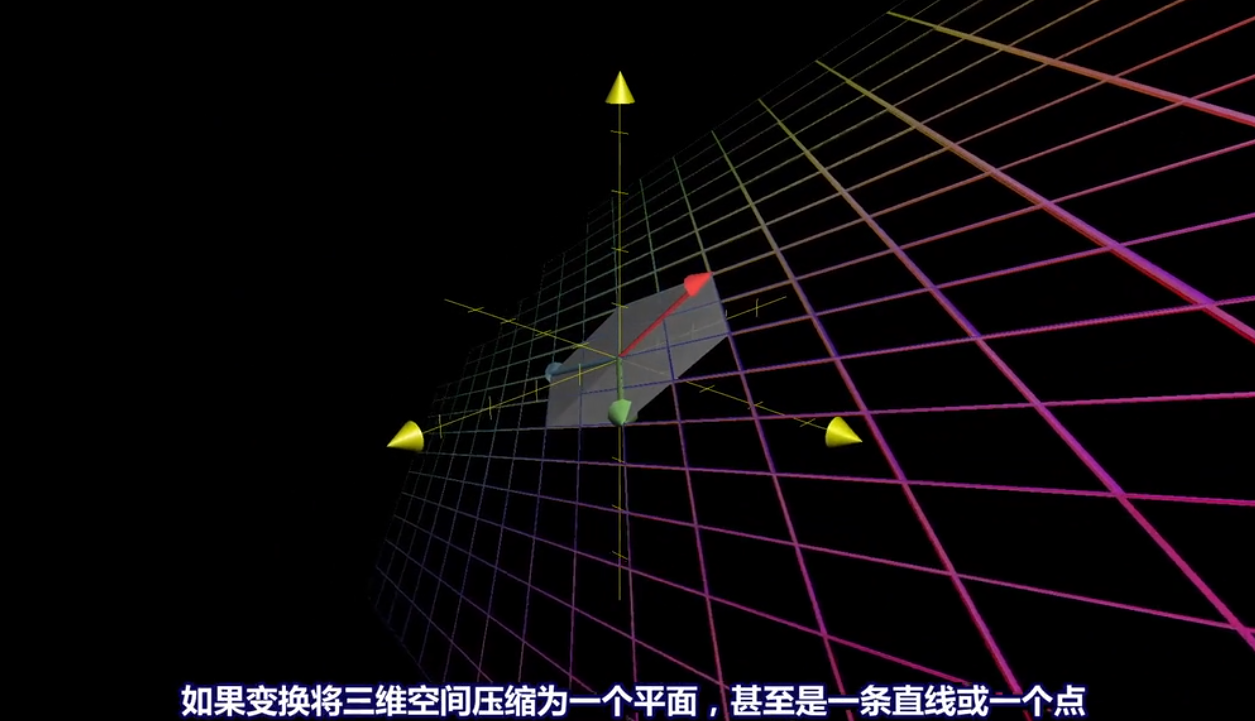

*****
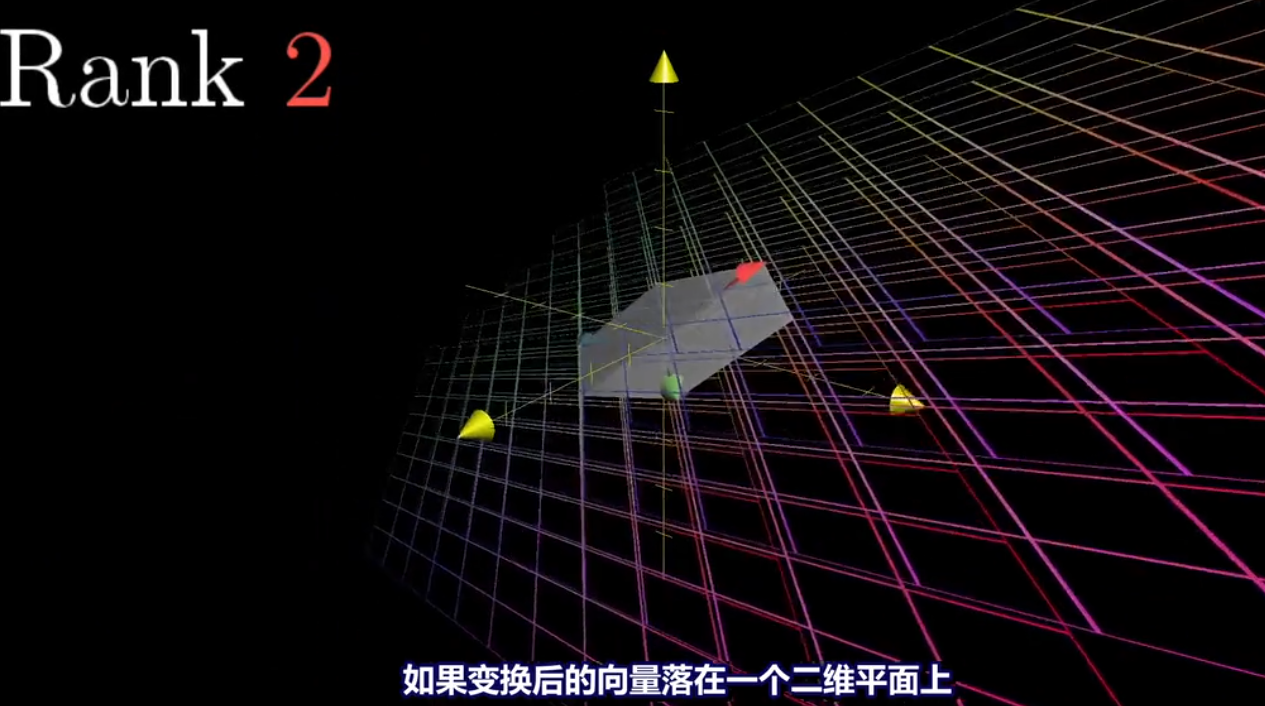
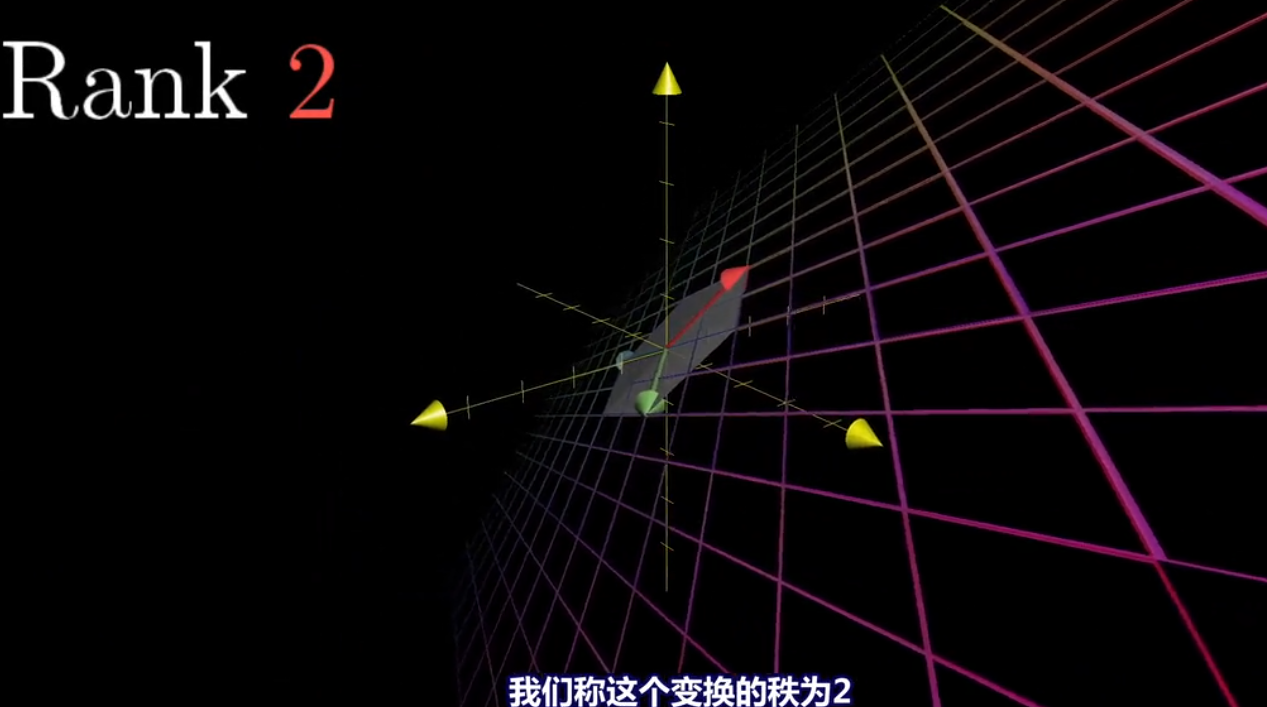
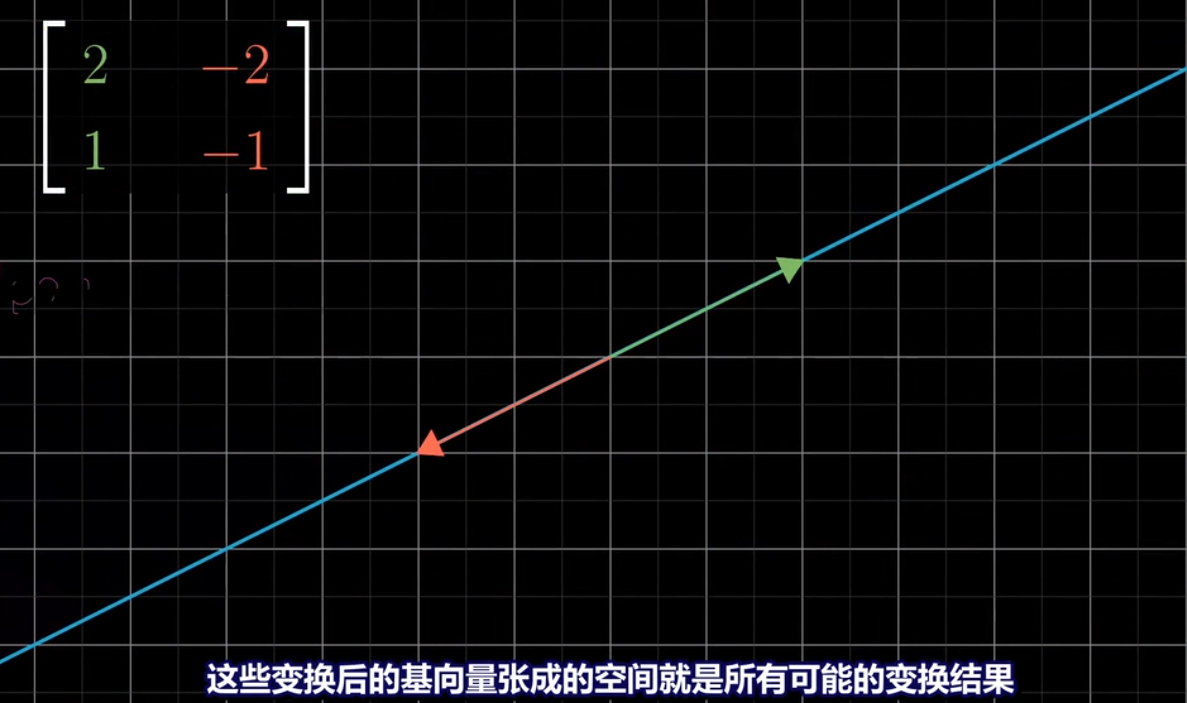
当变换将二维压缩成一条直线,称这个变换的秩为1


*****
基向量可以张成二维空间,且矩阵的行列式的不为零
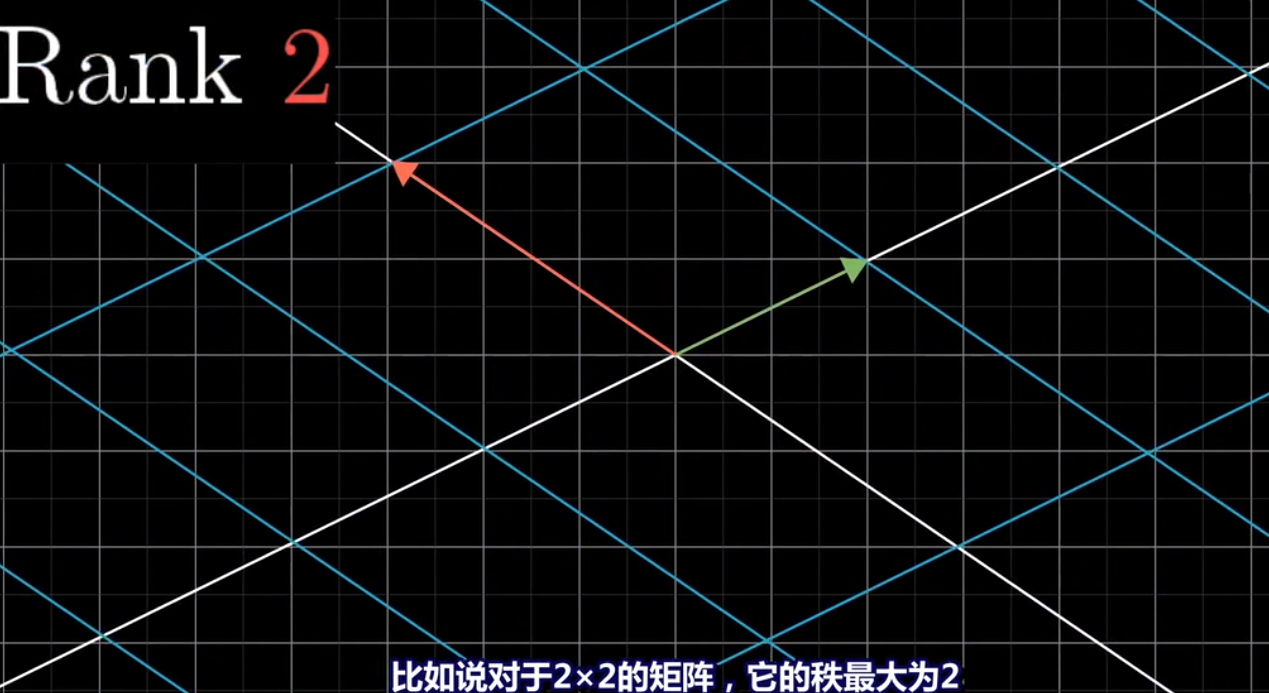
*****
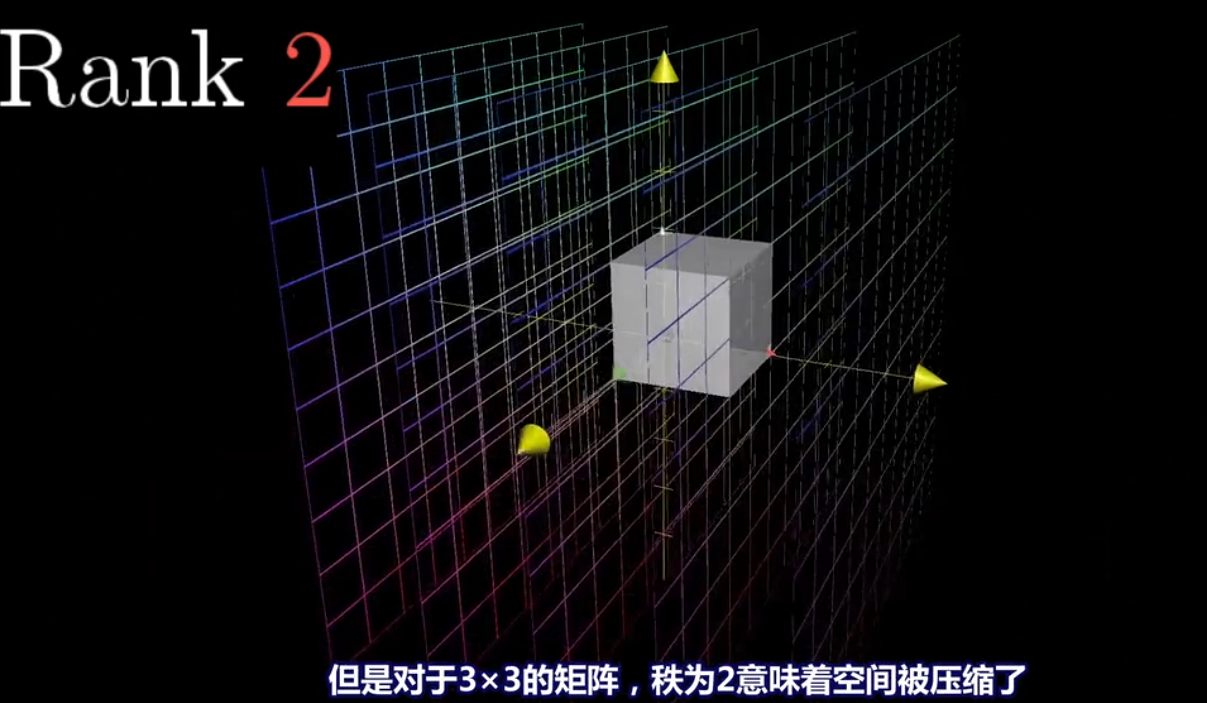
*****
所有矩阵变换变换结果的集合是矩阵的"列空间"

**原因**
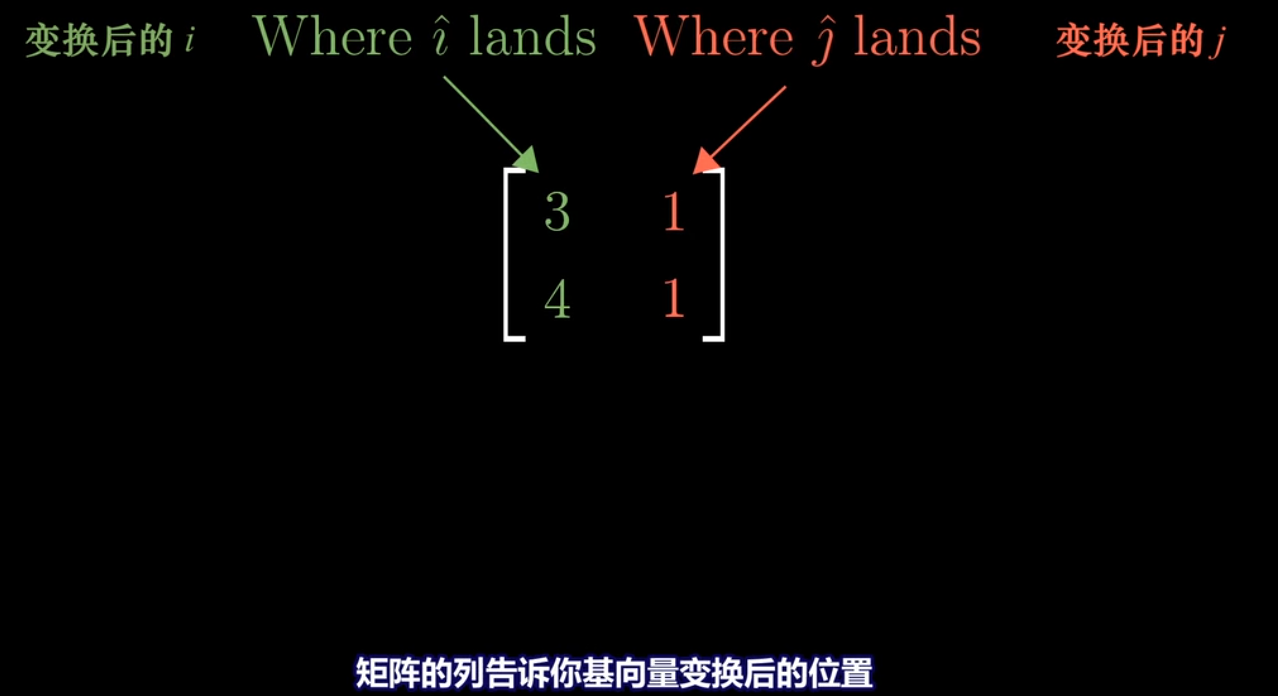

**秩的精确定义**




因为线性变换原点不变
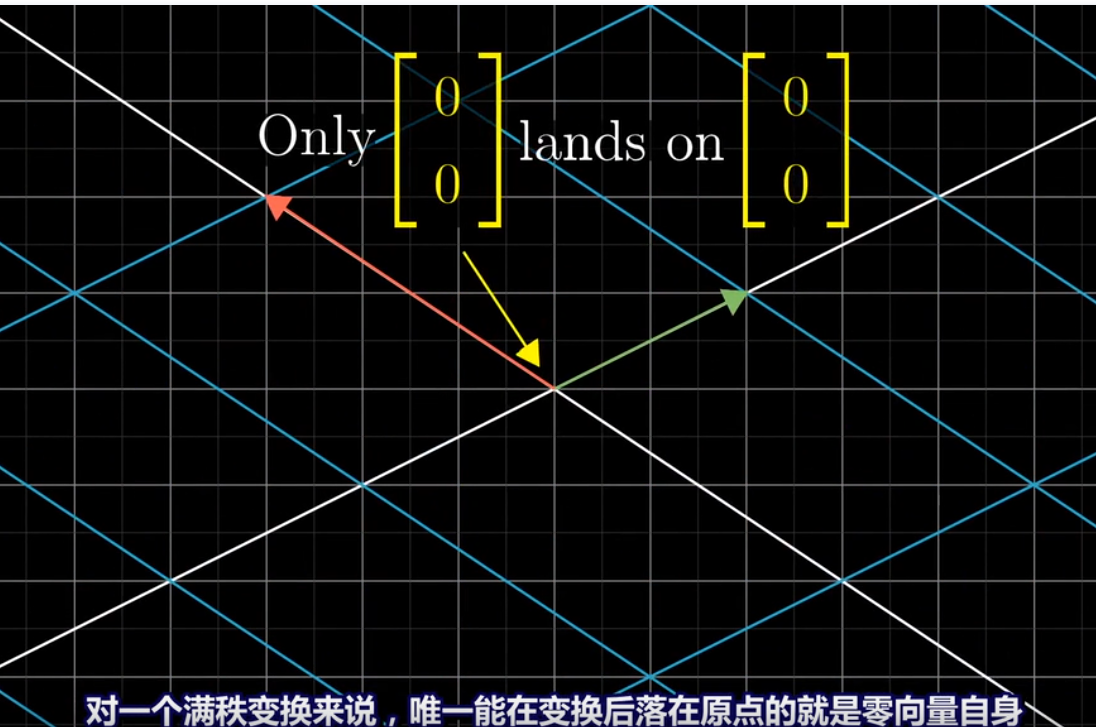
*****
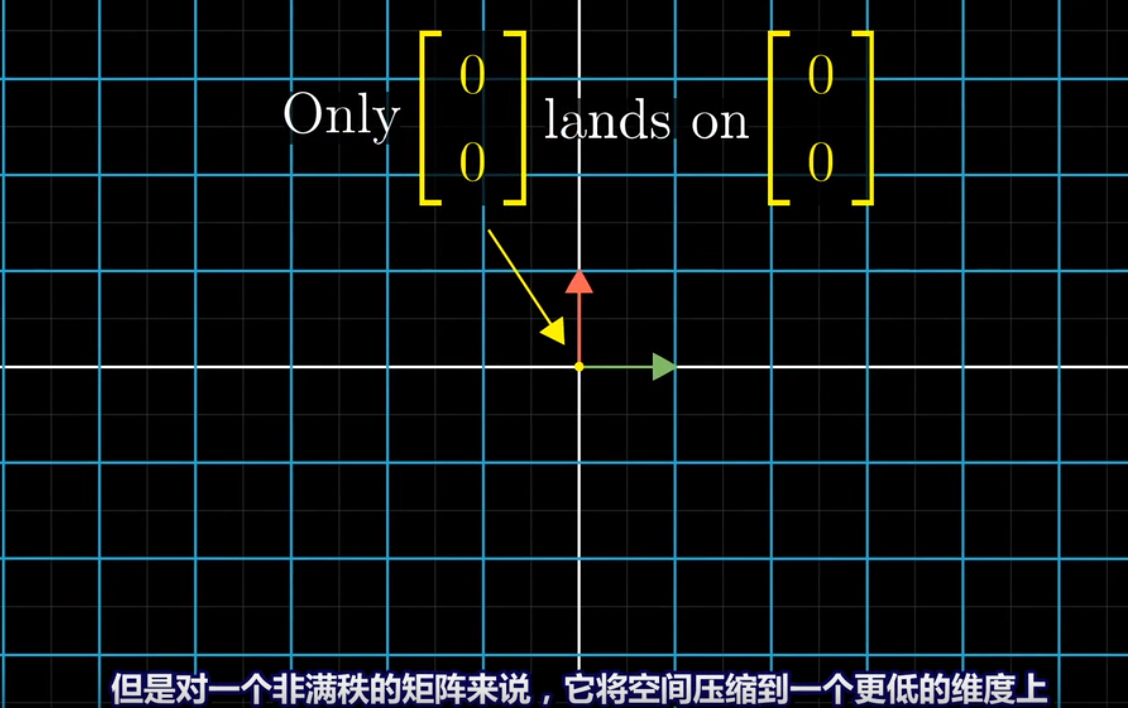
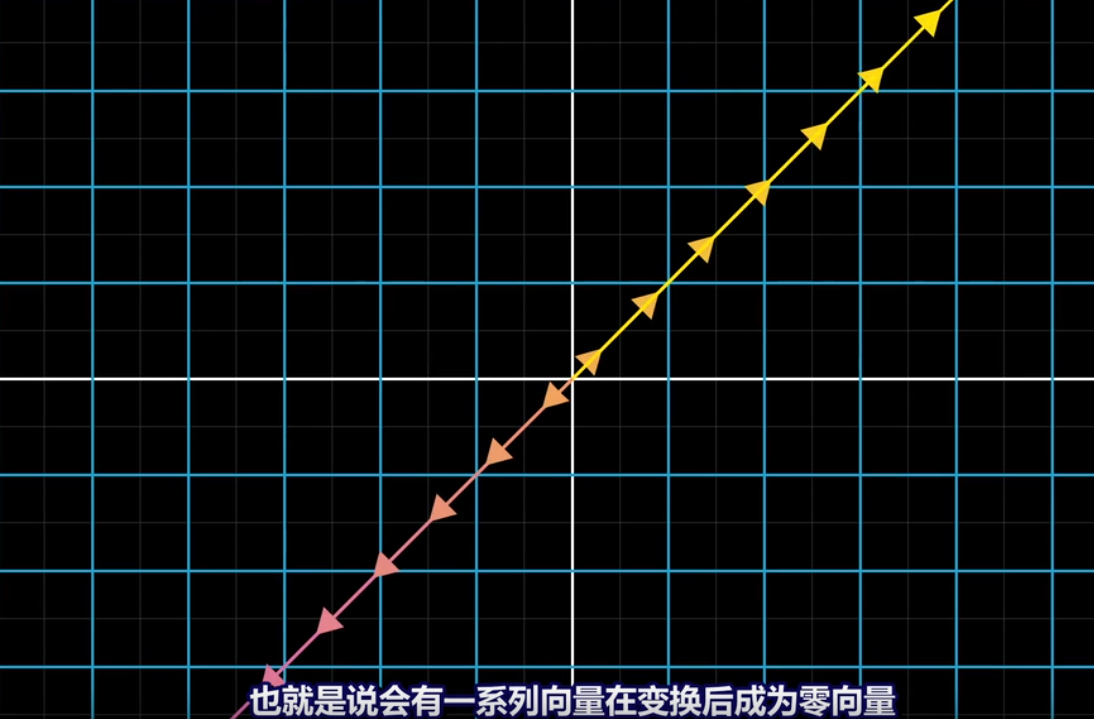
*****
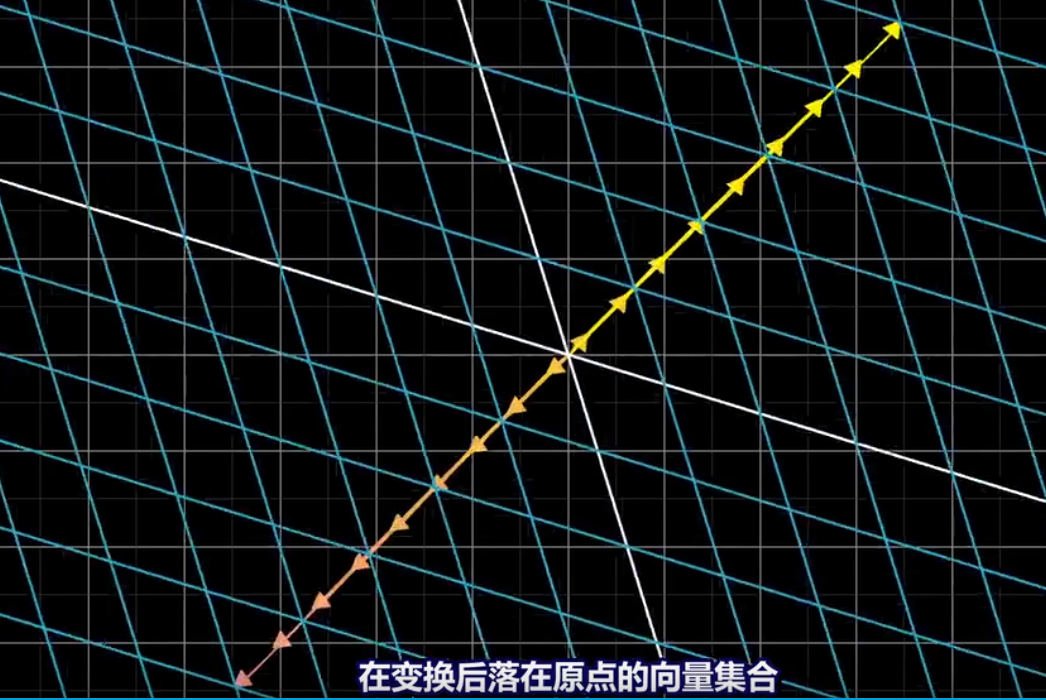
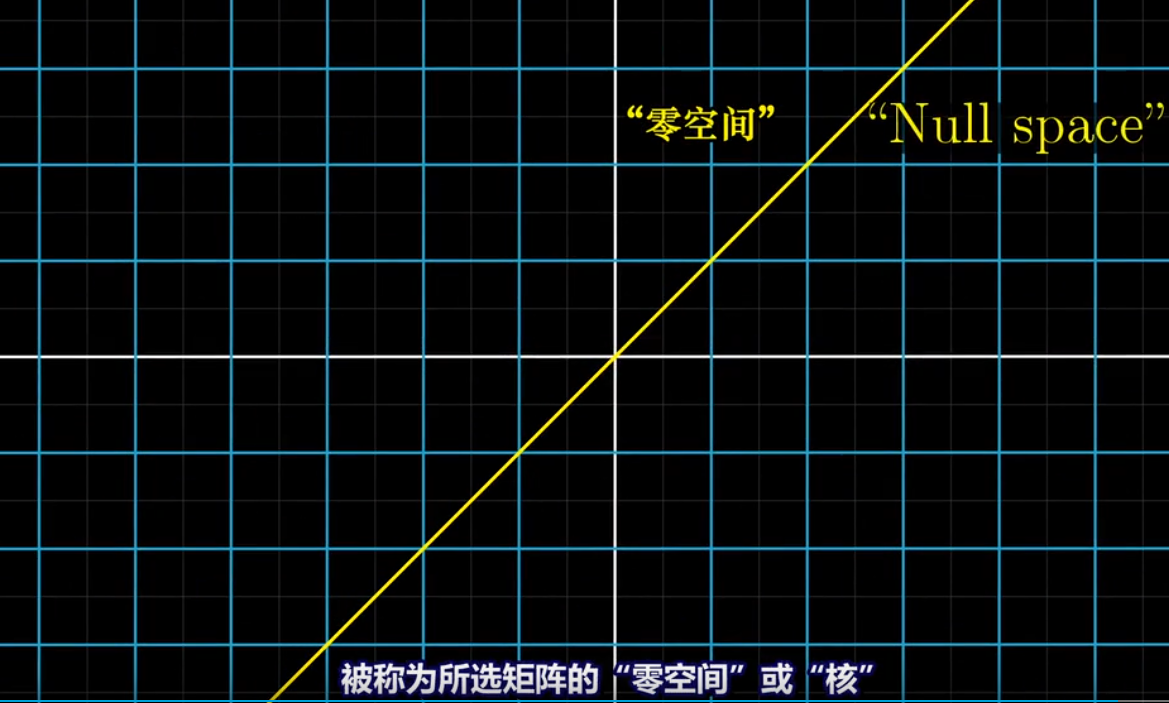
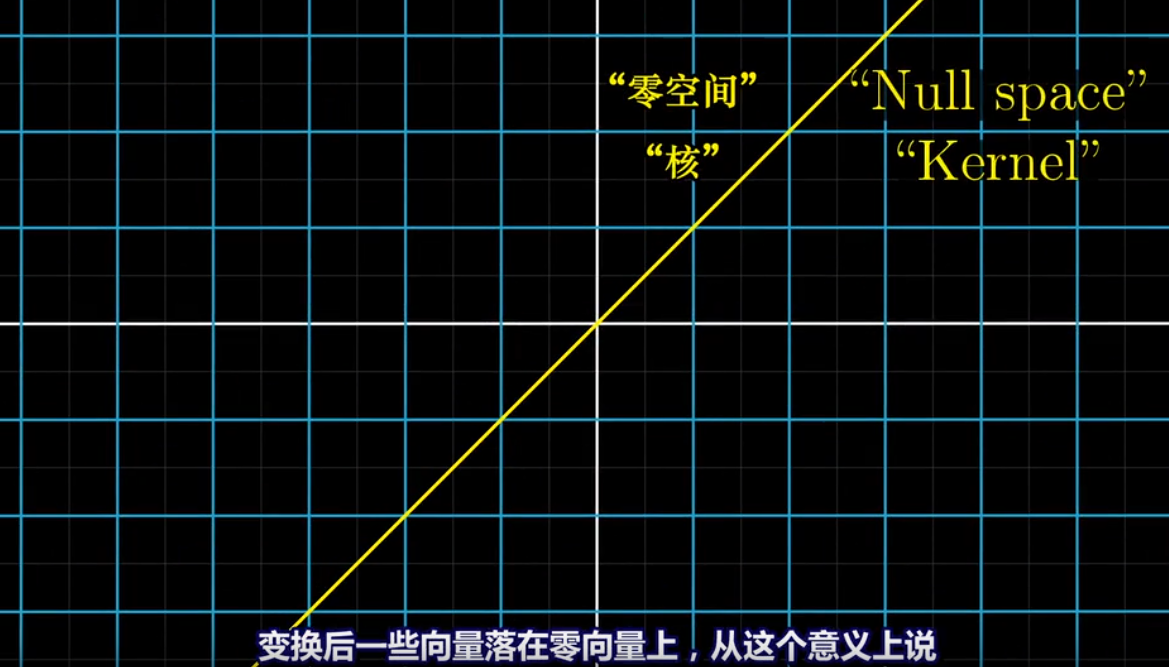

*****