**什么是特征向量?**
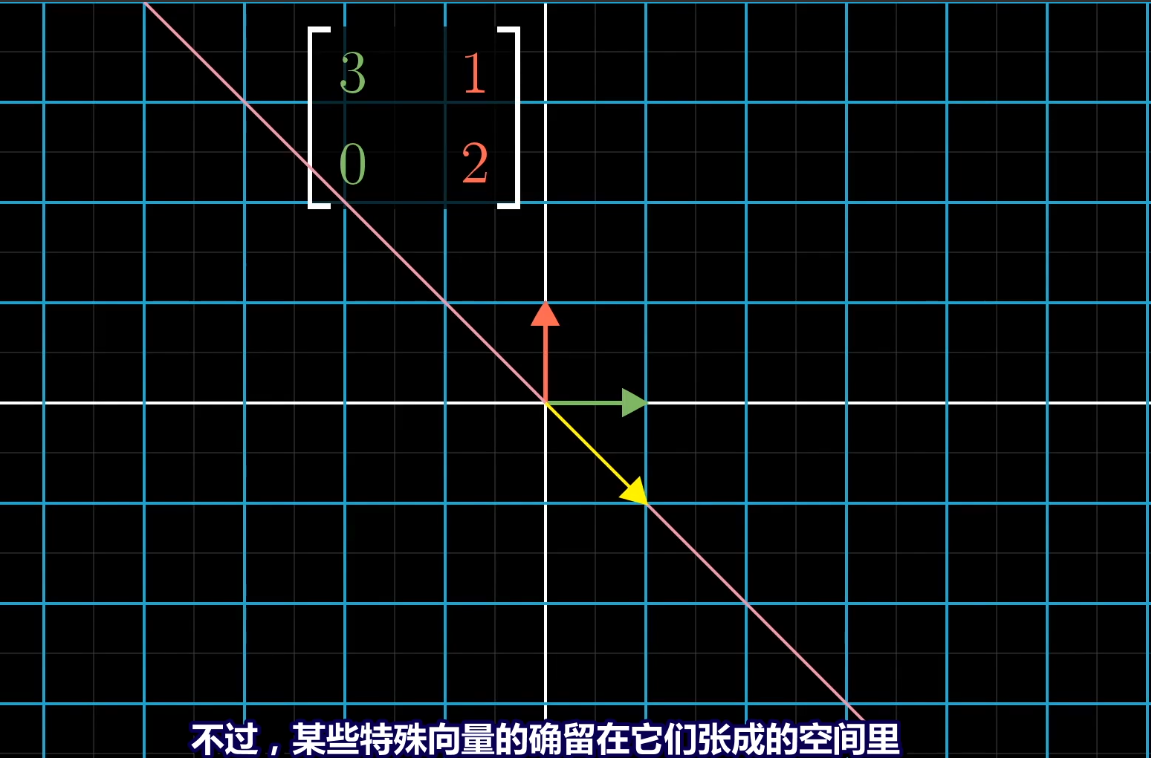
一个向量在一个线性变换M后,仍留在它所在的直线上,这条直线上的所有向量都是特征向量。如下图所示的黄色向量
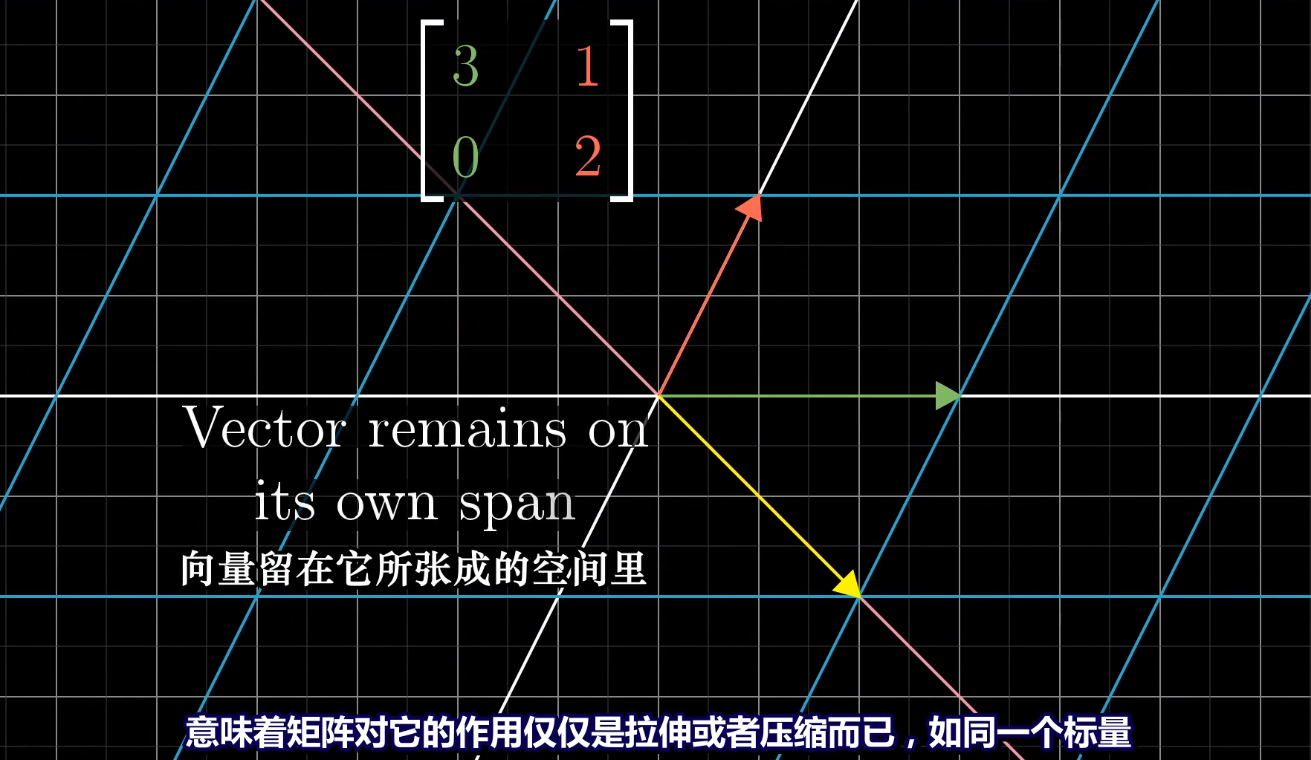
在这个变换中,i帽也是特征向量
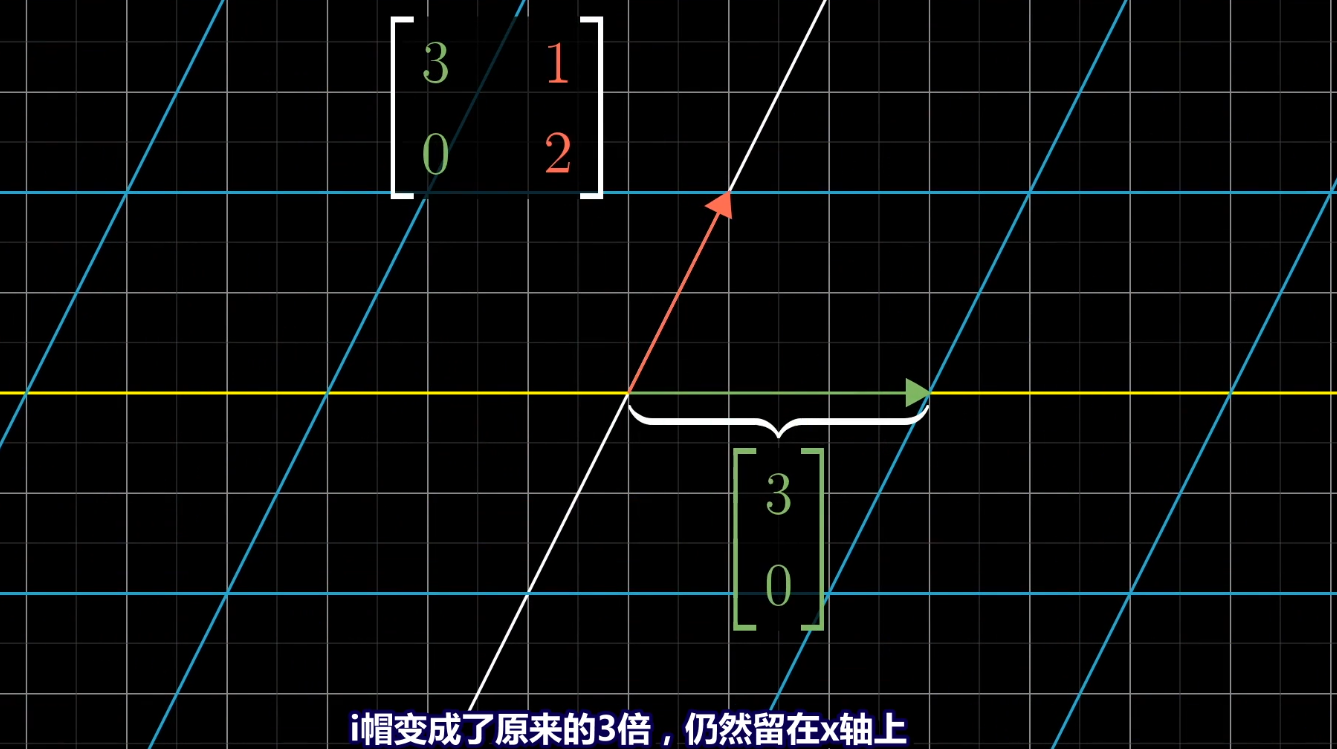
这个变换中,黄线和绿线上所有向量都是特征向量

**什么是特征值?**
特征向量被伸缩的比例就是特征值
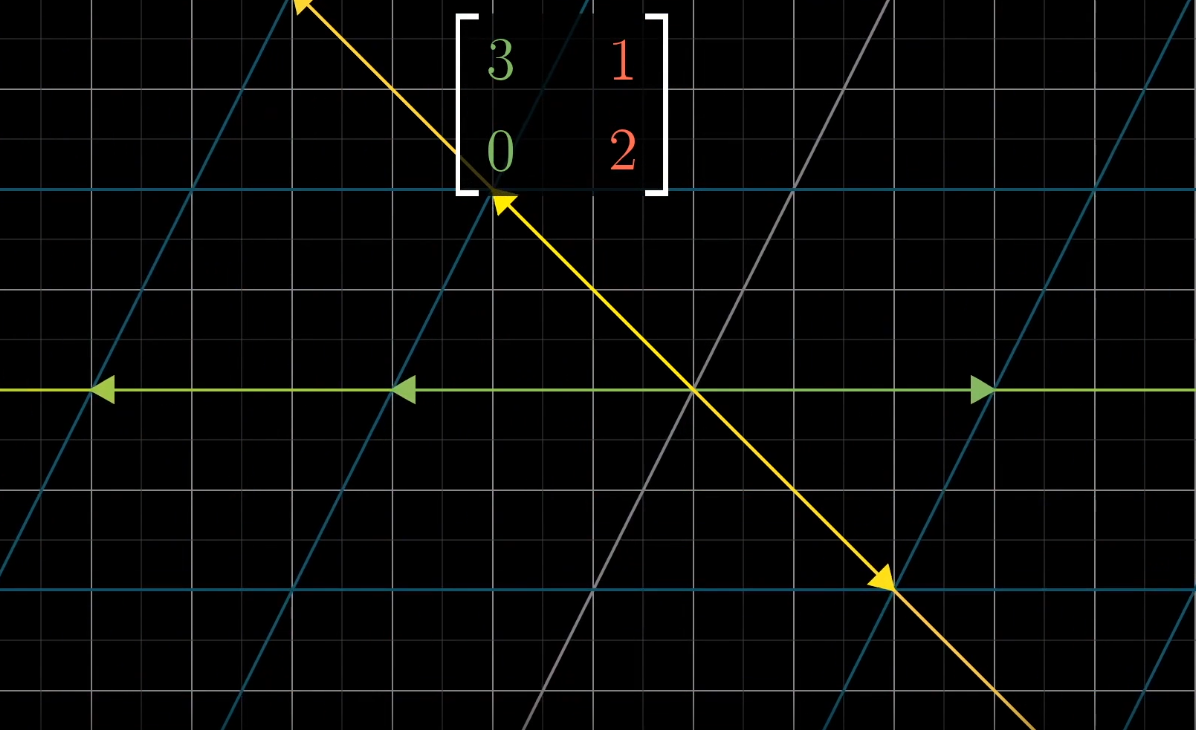
特征值可以为负,意味着特征向量向反方向伸缩,没有离开特征向量所在的直线
特征向量的用途,在3D旋转中,特征向量所在的直线是立方体的旋转轴,该特征向量的特征值必为1,因为只旋转,没有伸缩。
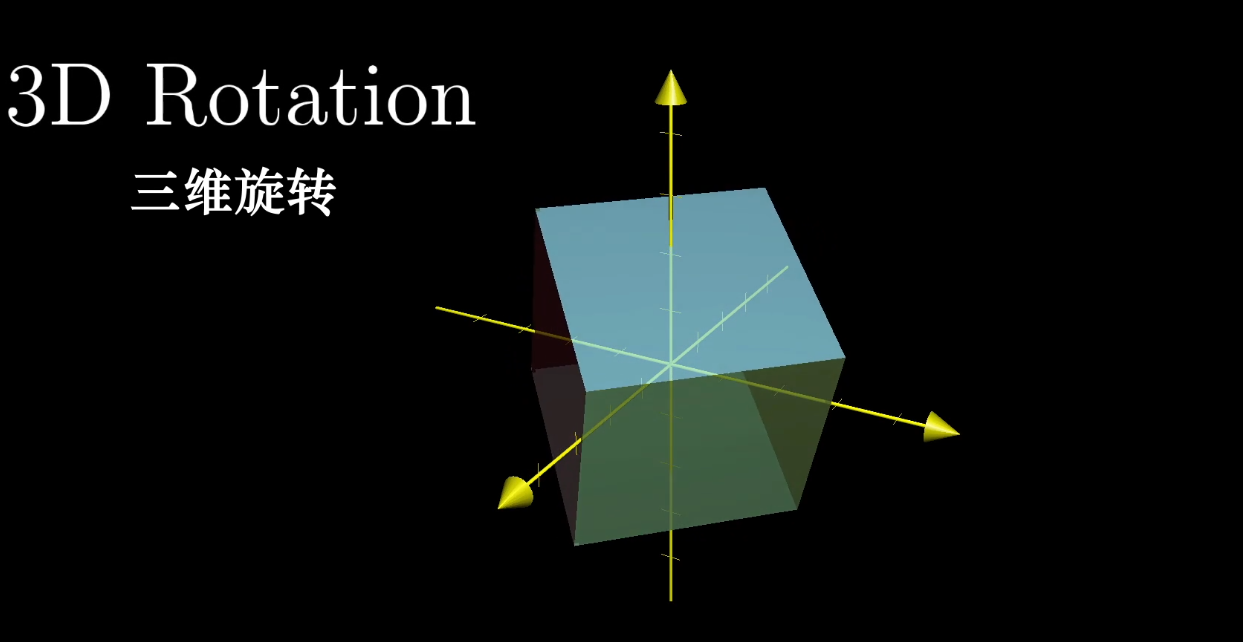
*****
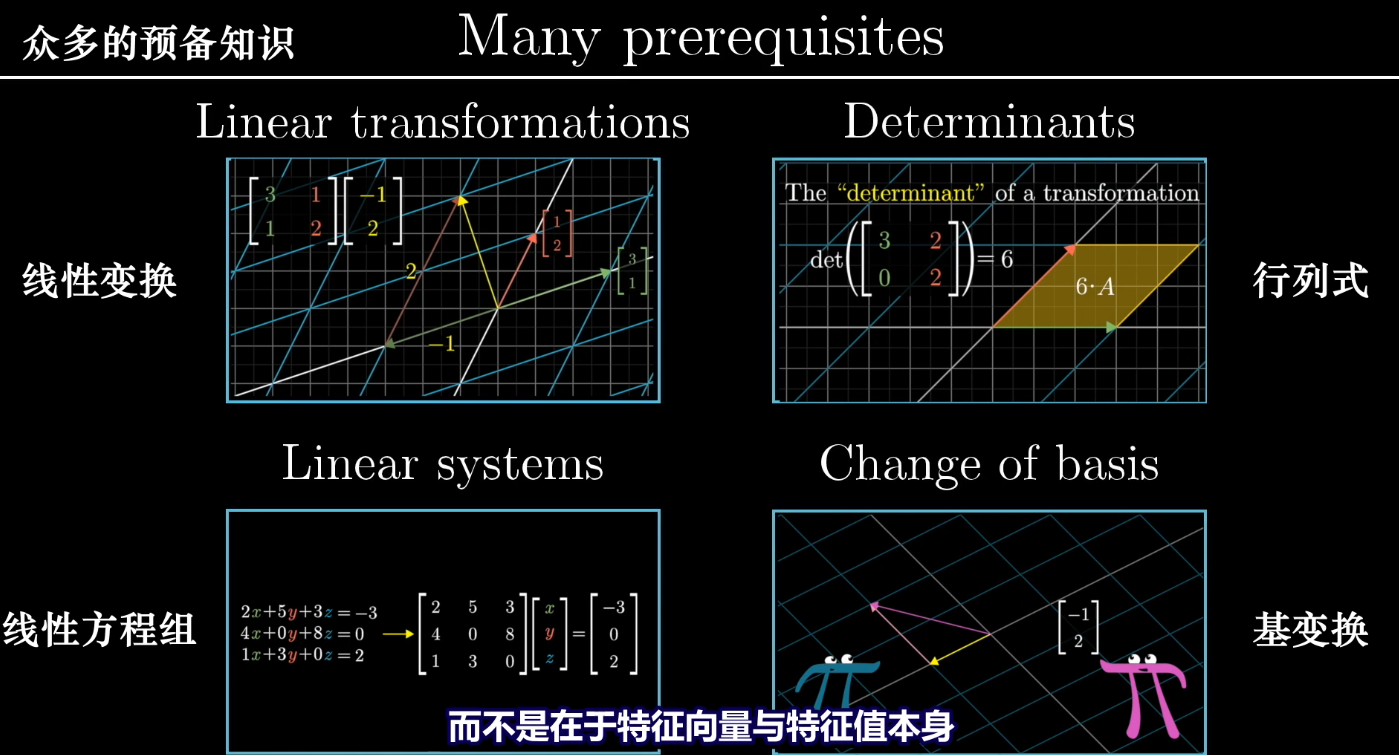
求出一个线性变换的特征向量和特征值,以能张成整个空间的特征向量组合为基向量,有助于我们更好的理解线性变换
*****
根据特征向量的概念可知等式
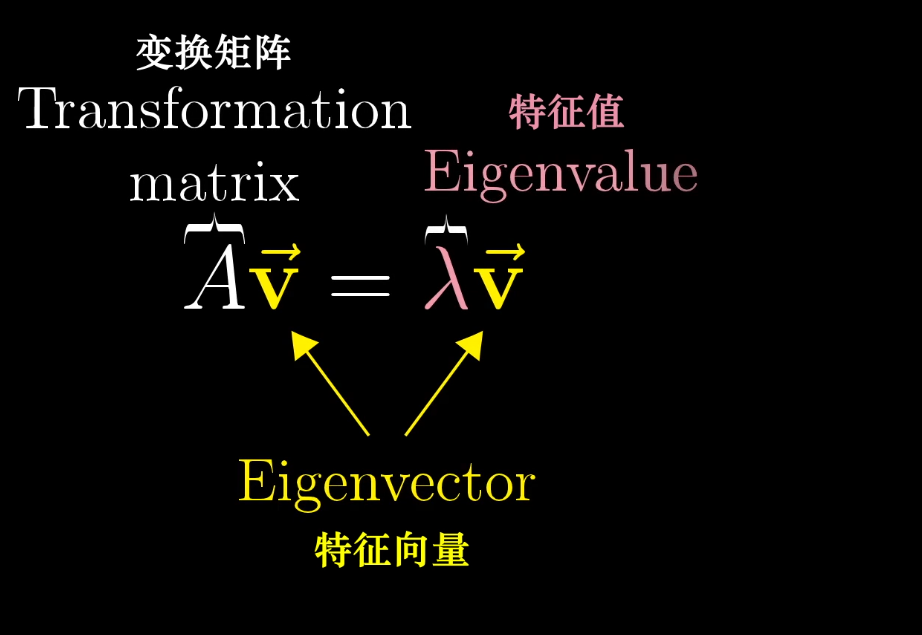
*****
一般已知变换矩阵A,求特征向量v和特征值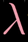
*****
向量v的数乘可以看做,向量v扩大了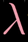倍,进行了基向量都扩大相同倍数的变换,如下图等于向量v左乘一个对角矩阵。



经过变换,如下图
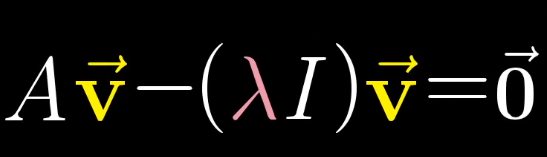

*****
如果v本身是零向量,上面等式恒成立,但这没有什么意义。我们的目的是找非零特征向量
*****
非零向量通过线性变换变为零向量,这个变换矩阵的行列式一定为0,矩阵将空间压缩到更低的维度上导致的。行列式为零意味着该变换将基向量围成的正方形面积或立方体体积为零。
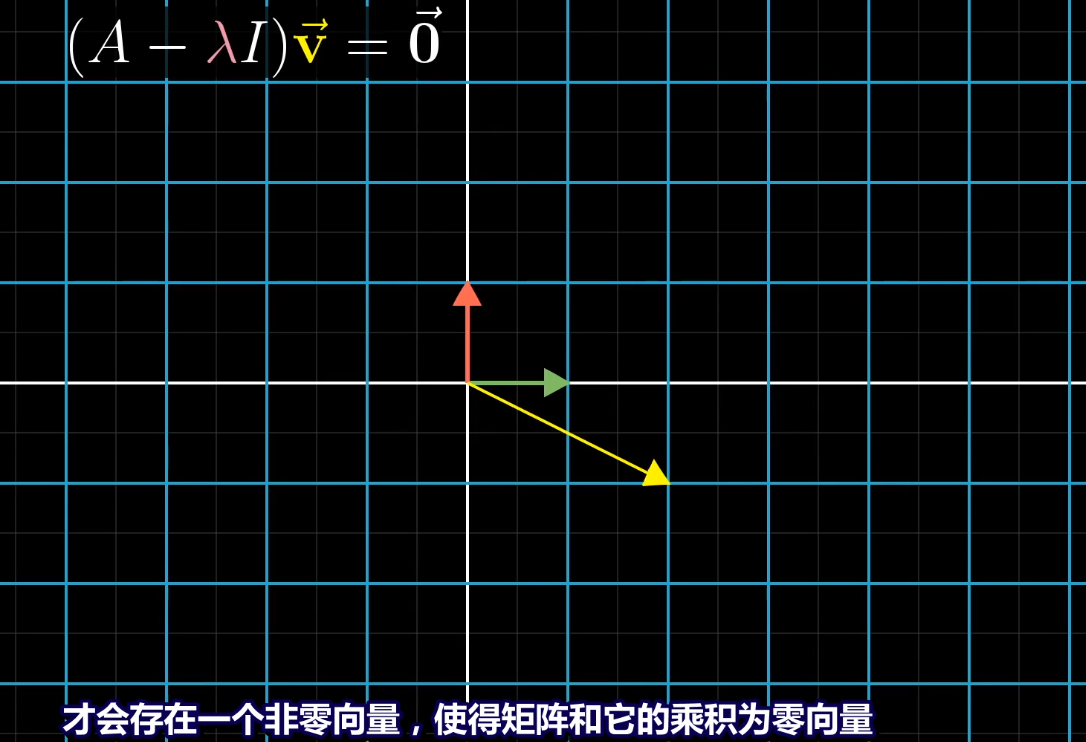
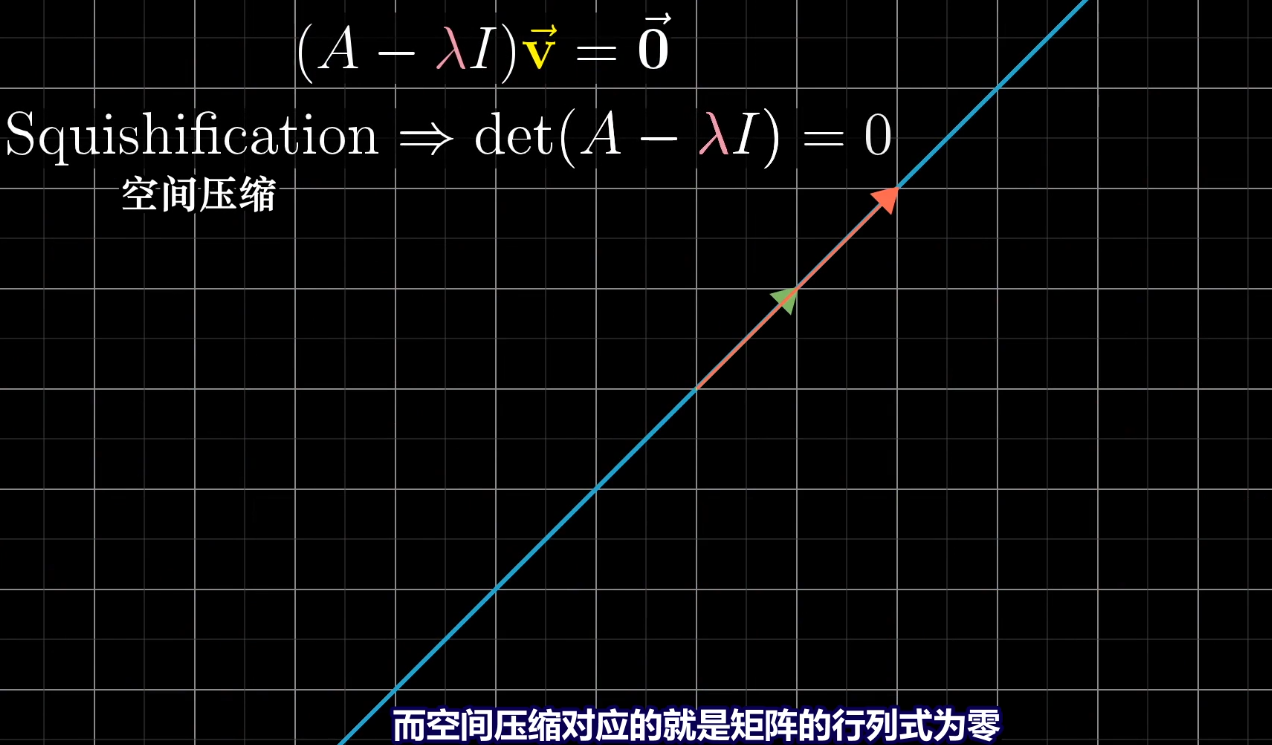
*****
对于下图矩阵,入改变时,矩阵也在改变,变换后基向量围成的面积也在改变,行列式在变。
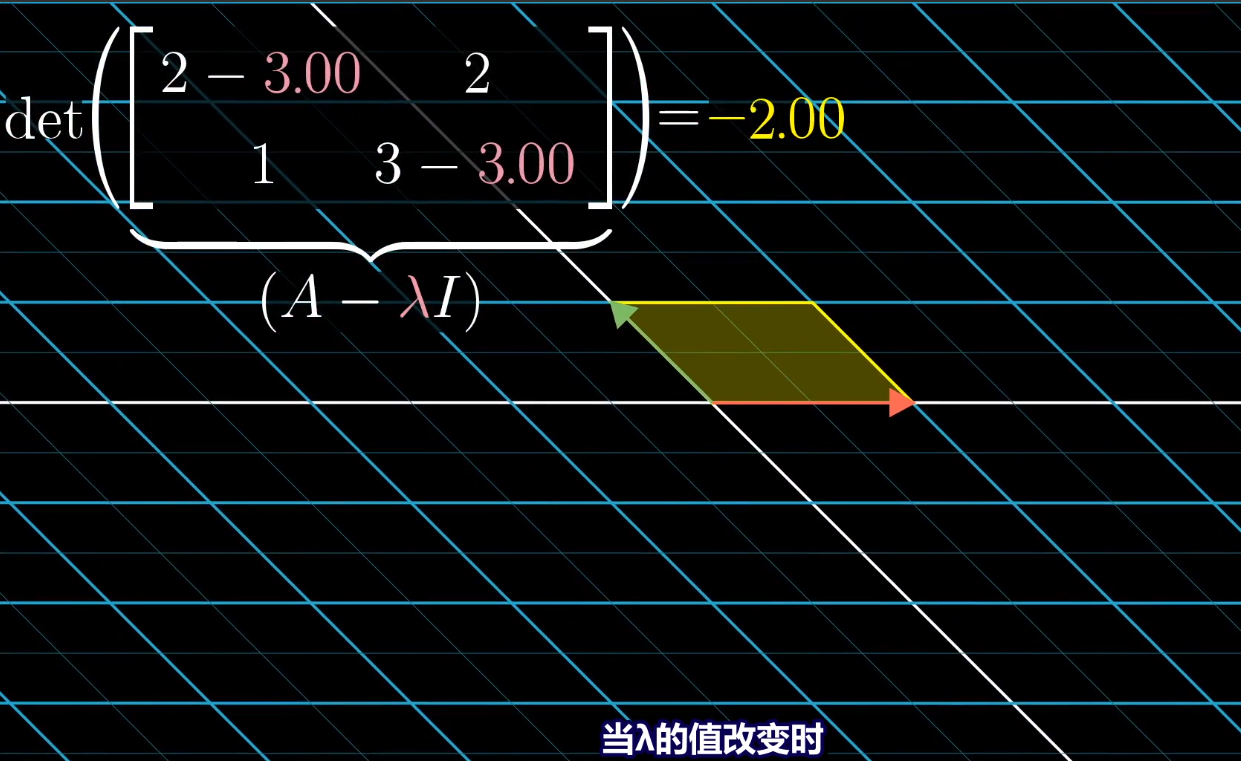
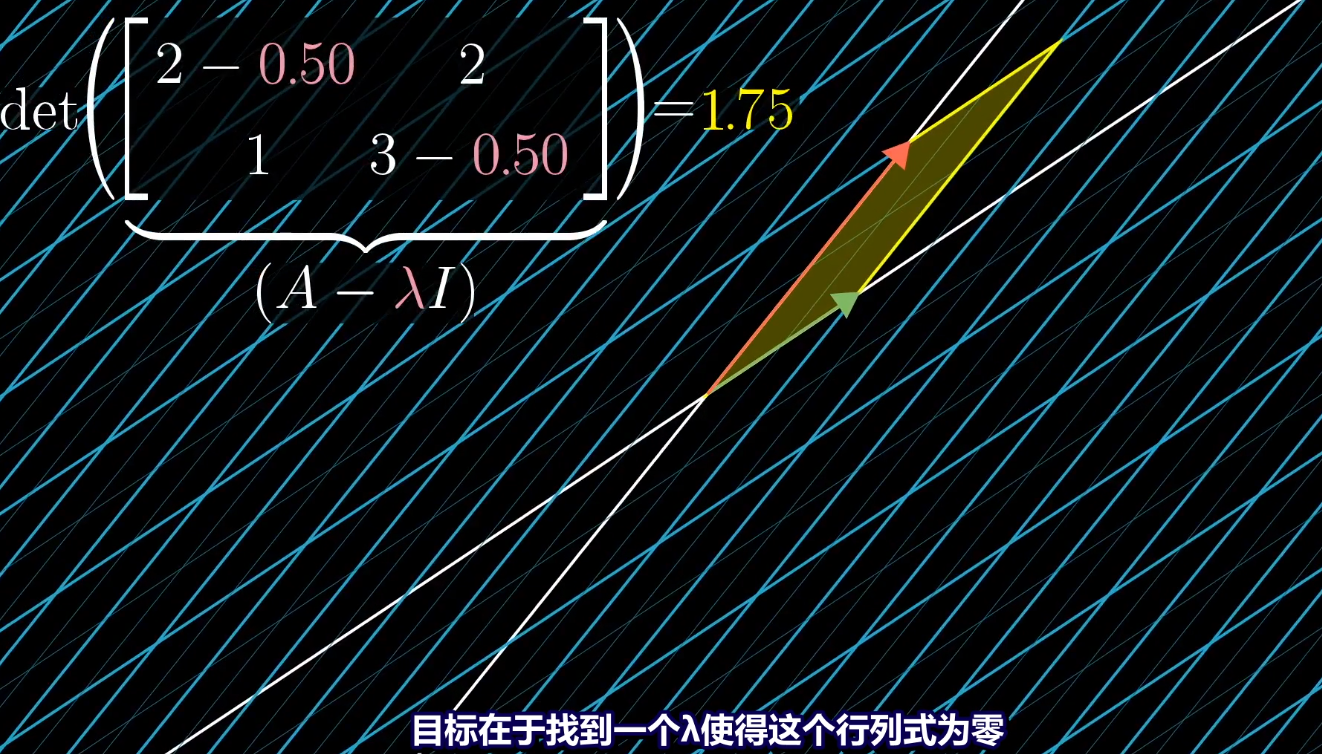

*****
**过程**
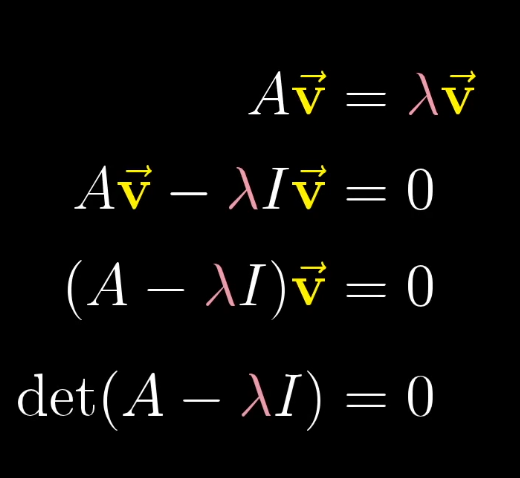
*****
**对于给定矩阵求解特征值**
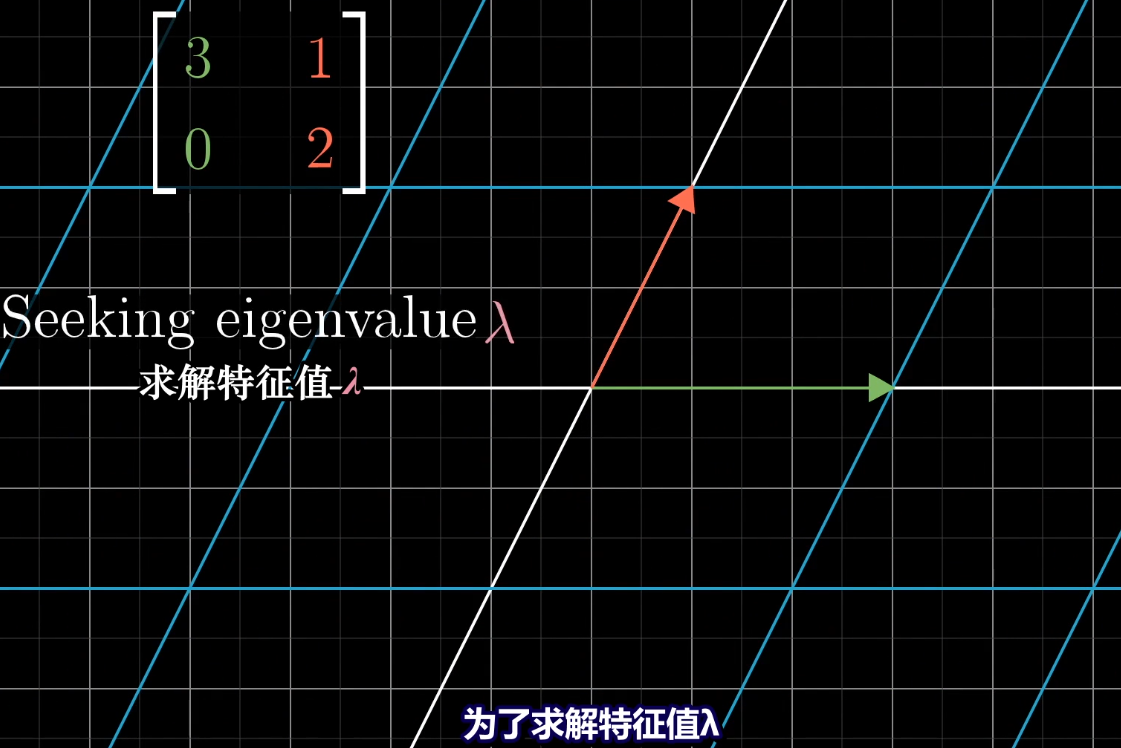

*****
**求解完特征值后求解特征向量**
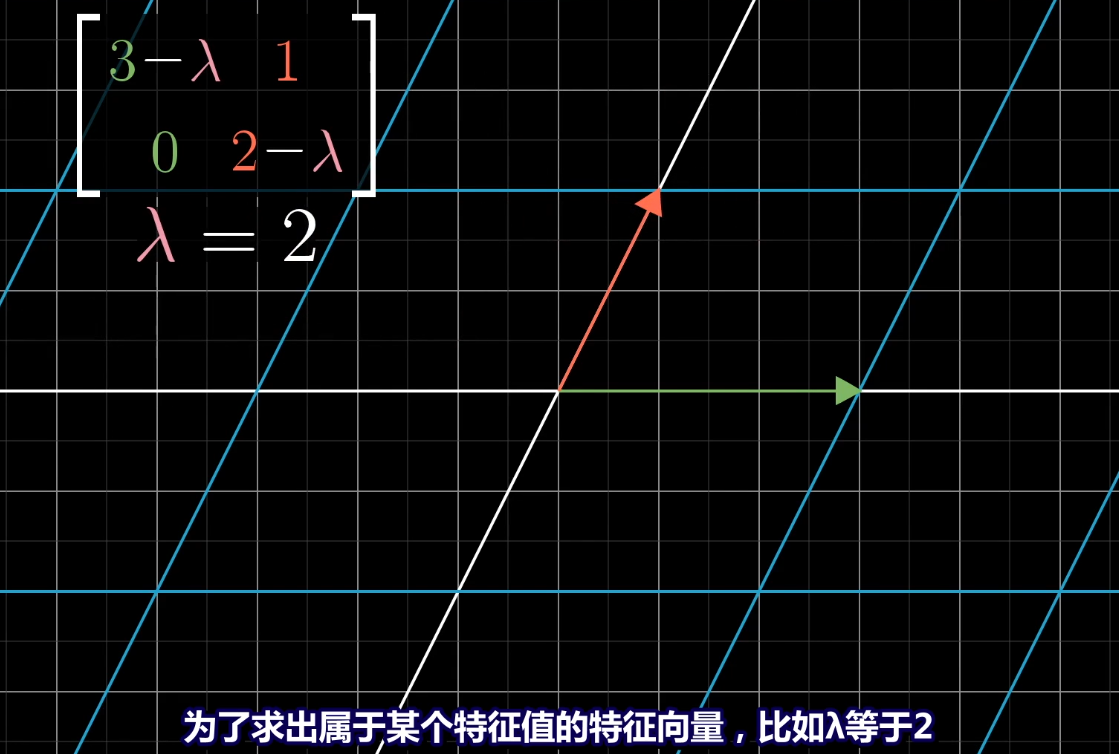
将入=0代入矩阵中
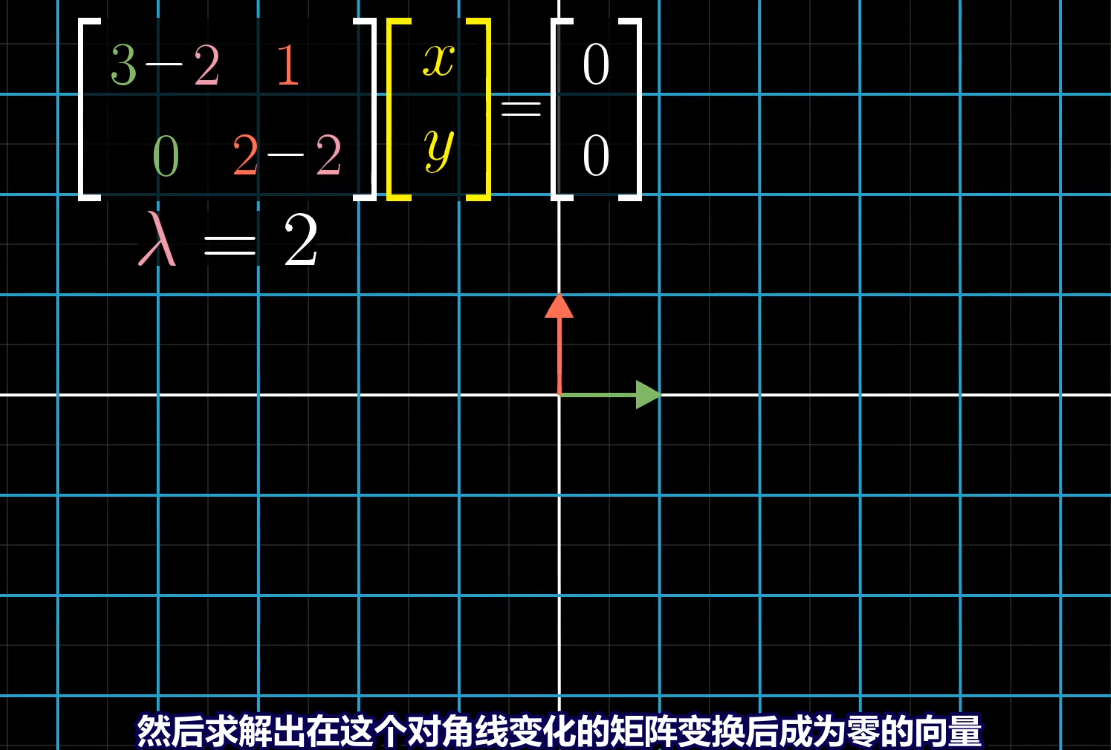
将上图矩阵相乘变为一个二元一次方程组求解,得y= -x。则y= -x直线上全是该矩阵变换的特征向量,特征值为2。
*****
有的线性变换没有特征向量,比如坐标系旋转90度。所有向量都不在原来的直线上。
*****
剪切变换的特征向量在x轴上

*****
**对角矩阵的特征向量**
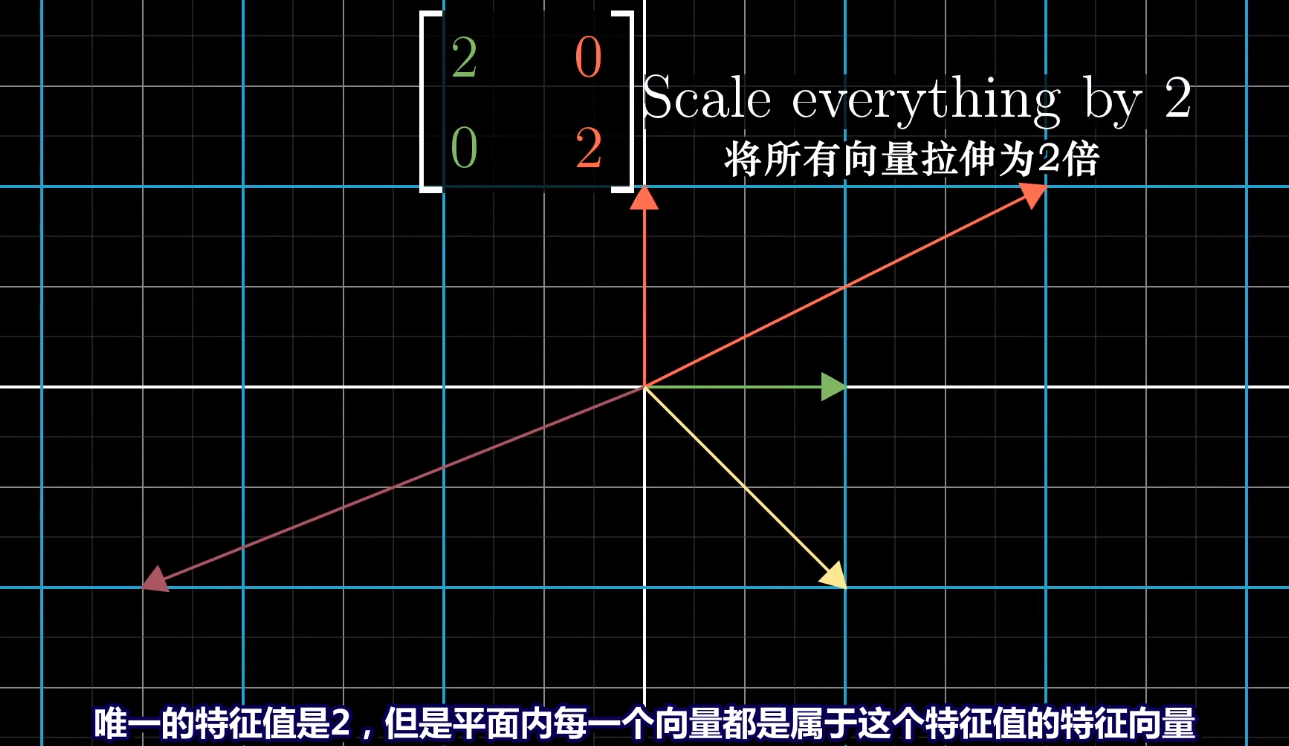
*****
**特征基**

每个对角元是该基向量在所在直线上特征向量的特征值

*****
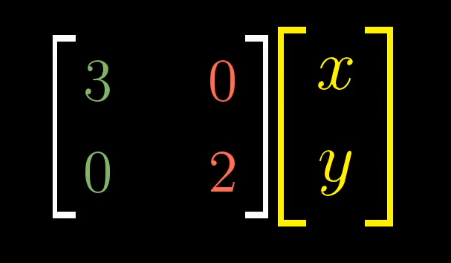

*****
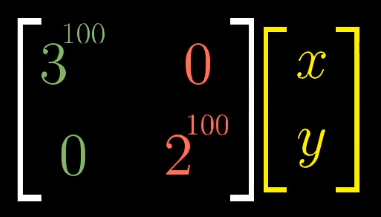
*****
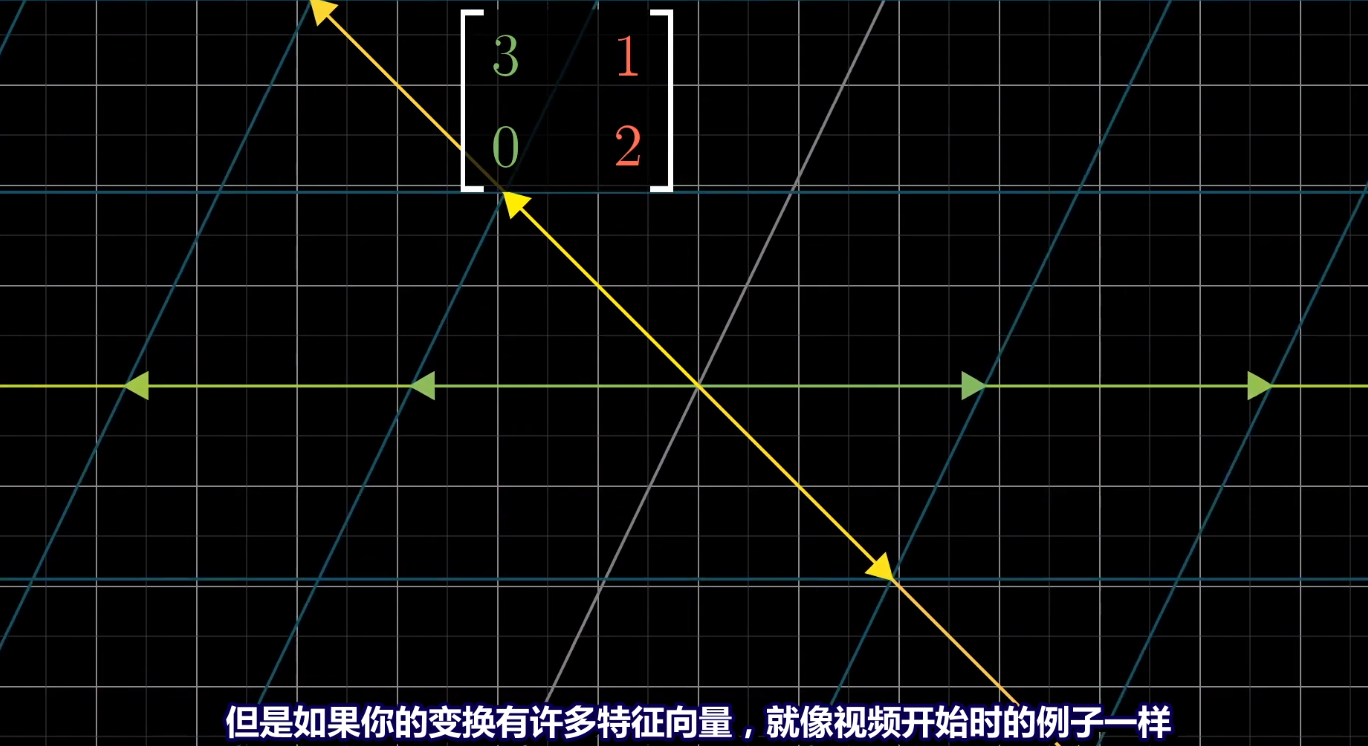


特征向量作为基向量进行线性变换,基向量只用进行伸缩或反向,不用旋转。
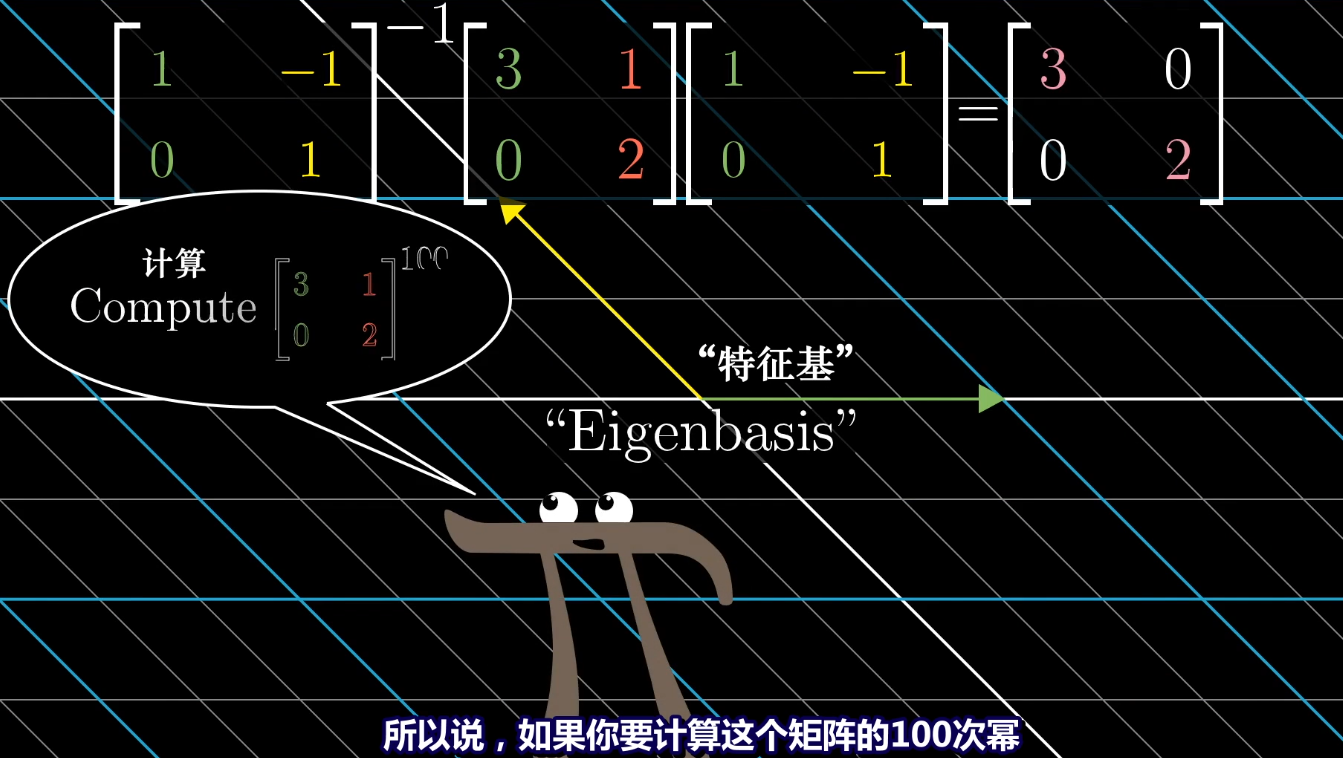
**用特征向量作为基**
用A-1MA求出以特征向量为基向量的坐标系上的线性变换。
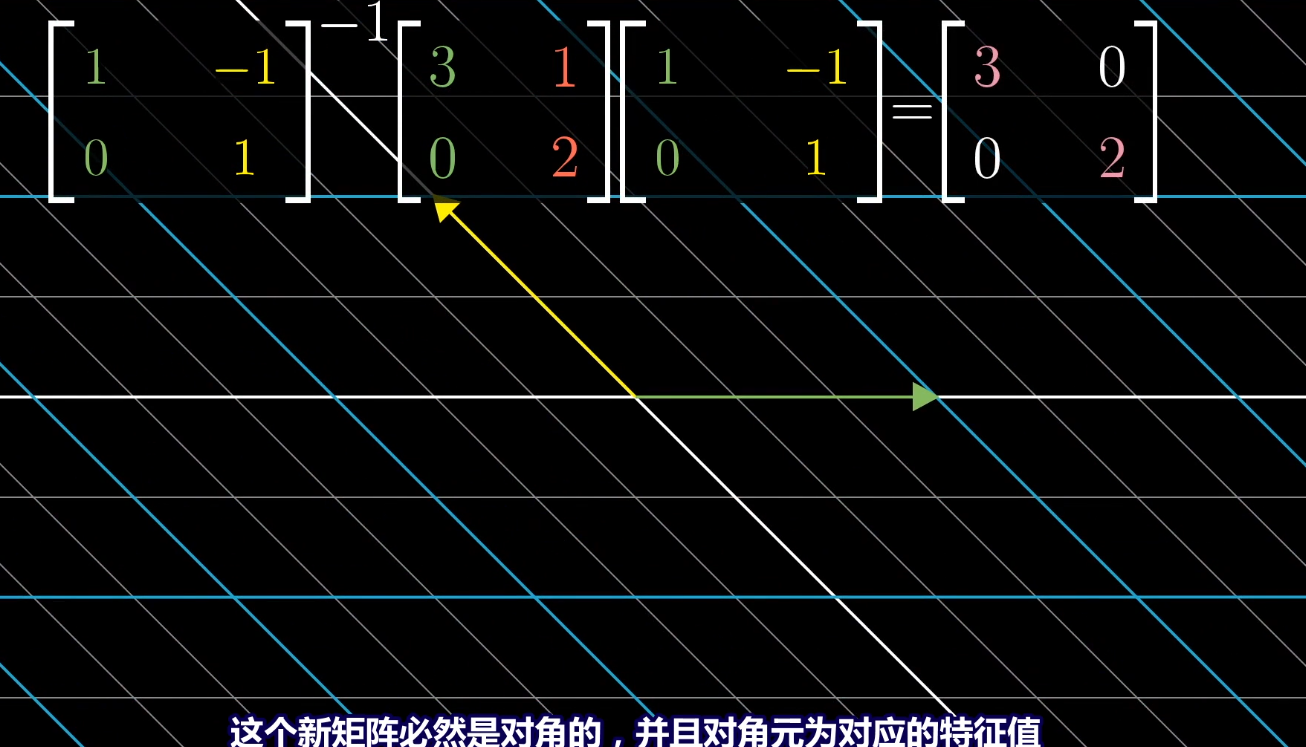
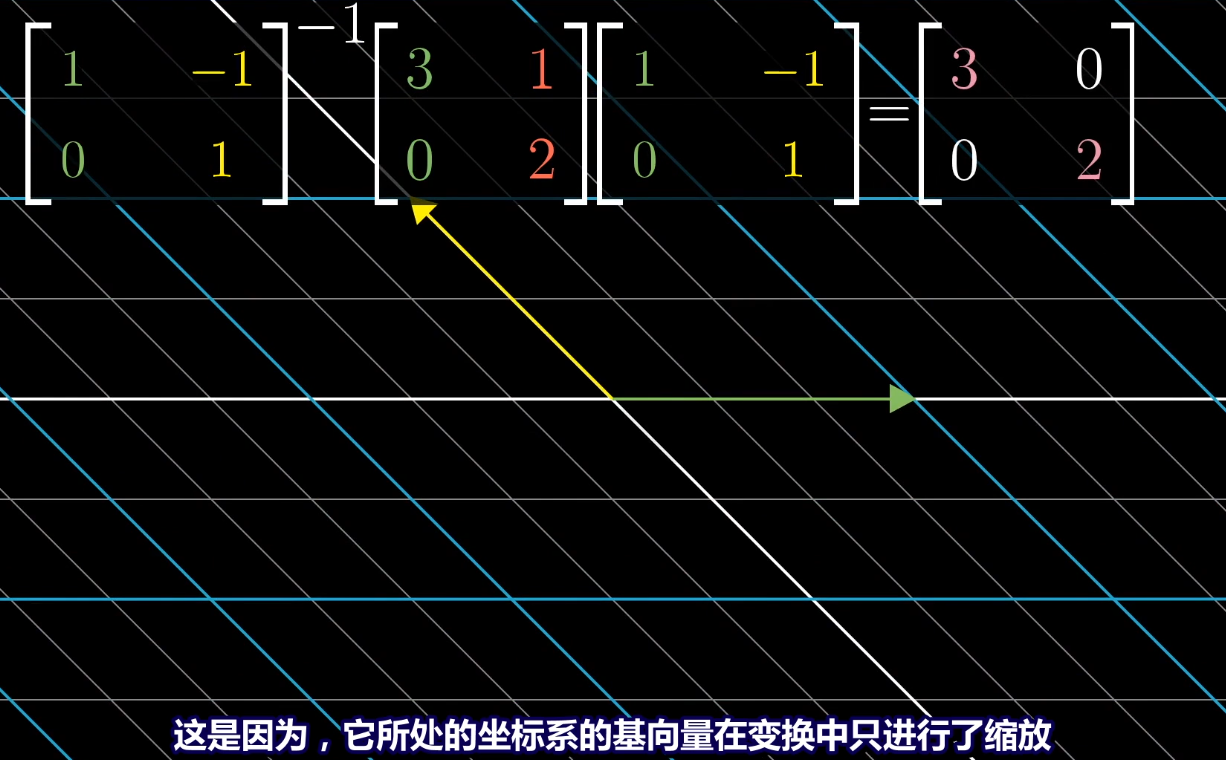

特征基对应于原坐标某个矩阵变换只是缩放基向量的变换
*****
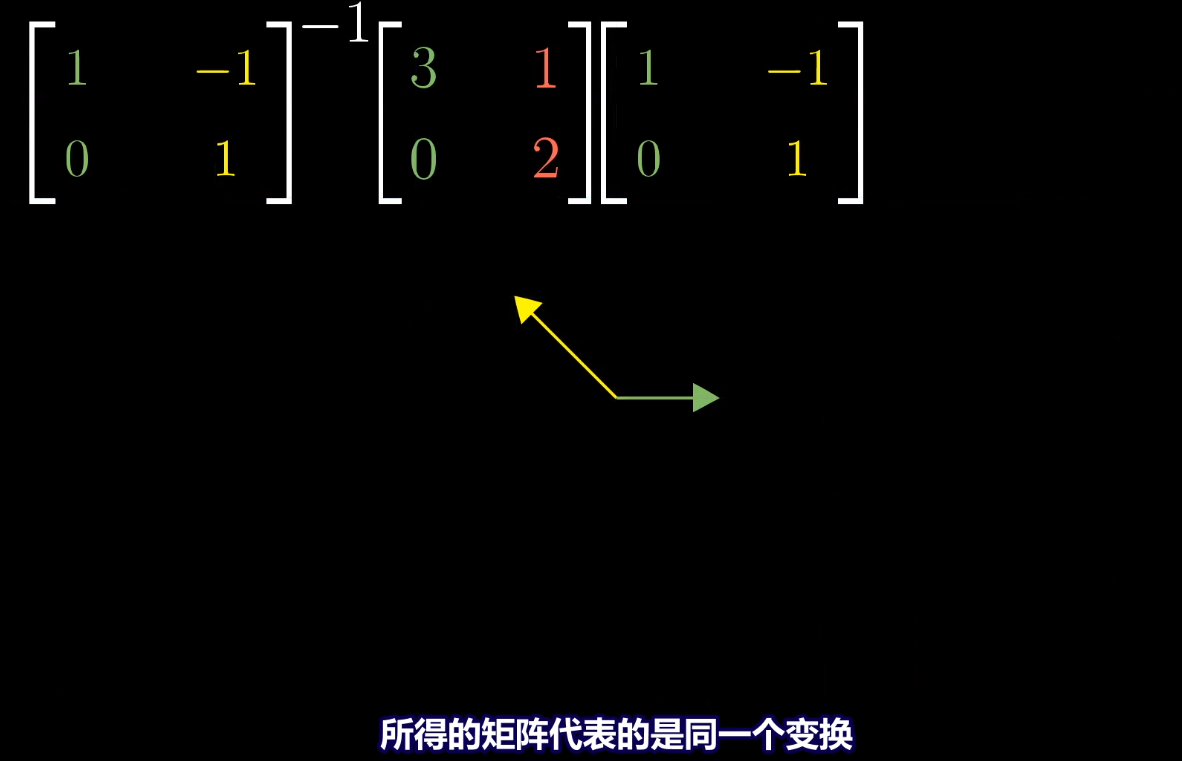
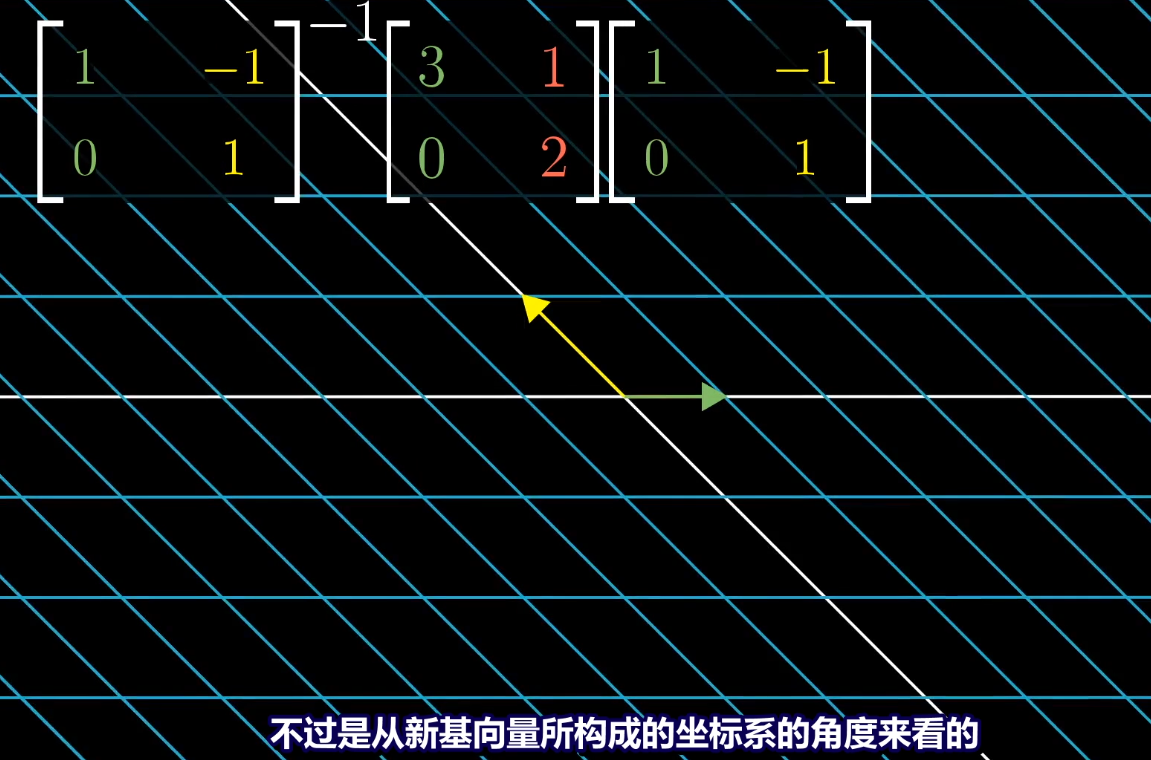
*****
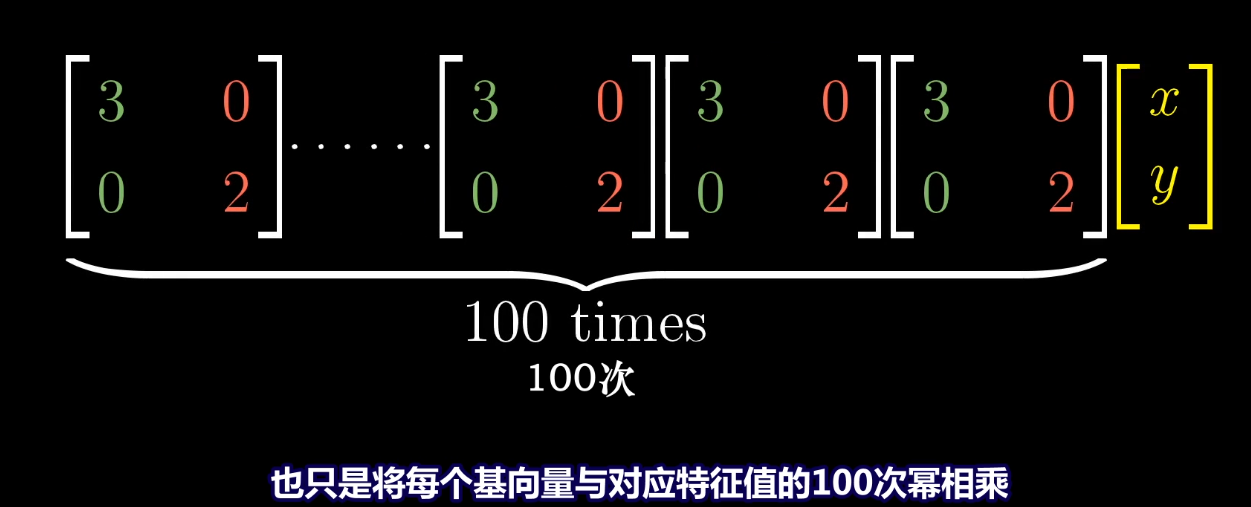
算某个矩阵变换的100次幂,找到该矩阵的特征基,对特征基下的相同矩阵变换(对角矩阵)求100次幂,然后对对角矩阵100次幂的复合变换,左乘矩阵A(特征基矩阵),变为原坐标系下的矩阵变换