# 第八节叉积理解不清楚
# https://blog.csdn.net/nbl97/article/details/80582027
*****
表示在二维空间中的一个向量
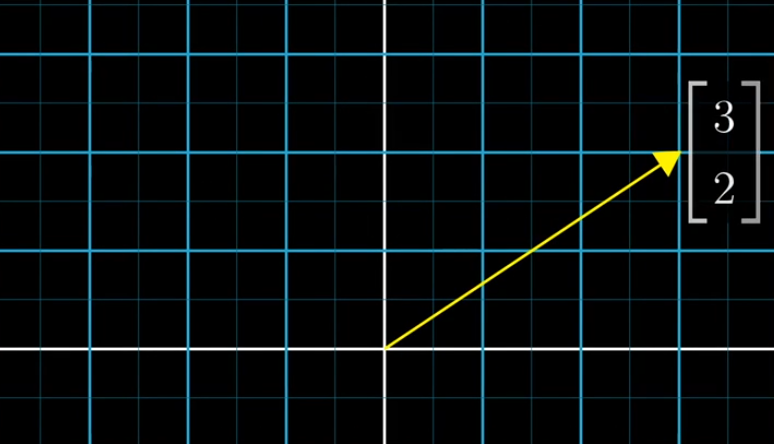
*****
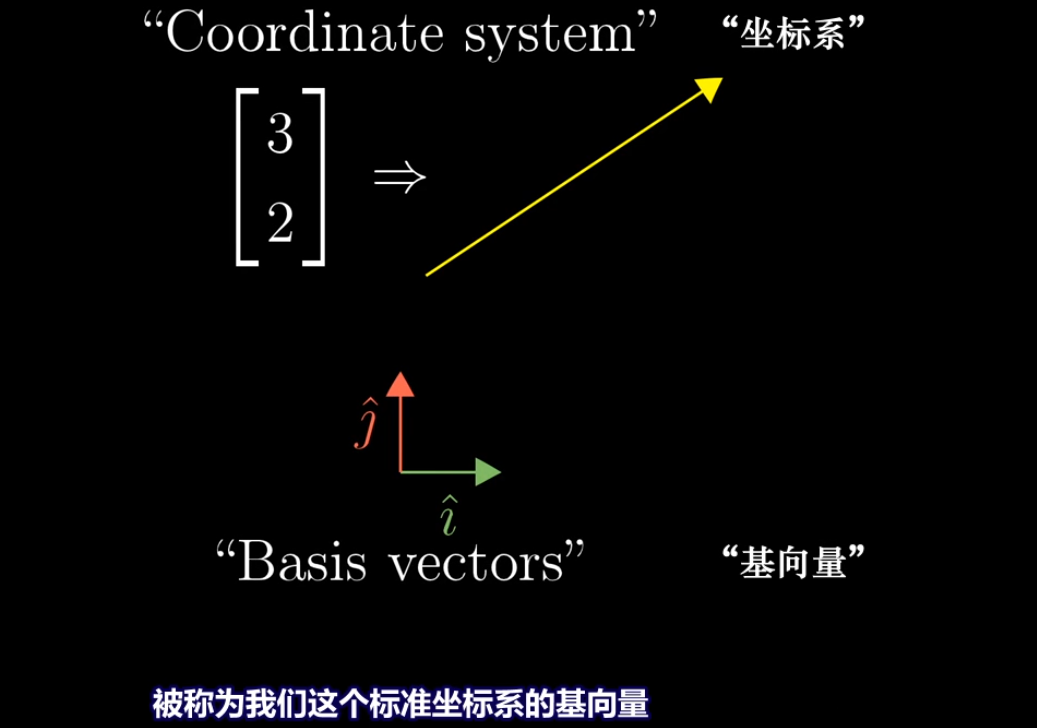
**2*2矩阵的解释**
2*2矩阵可以看做包含了线性变换信息的两个向量,(变换后的 i 向量) 和 (变换后的 j 向量)。
*****
两个2*2矩阵相乘可以看做对M1的两个向量做线性变换得到两个新的向量。
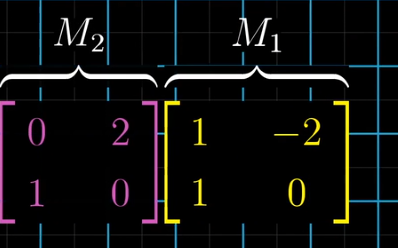
*****

*****
在另一个坐标系B中的基向量为b1和b2,两个基向量在坐标系B中坐标为b1(1,0) 和 b2(0,1)。在原坐标系中b1和b2的坐标为如下图
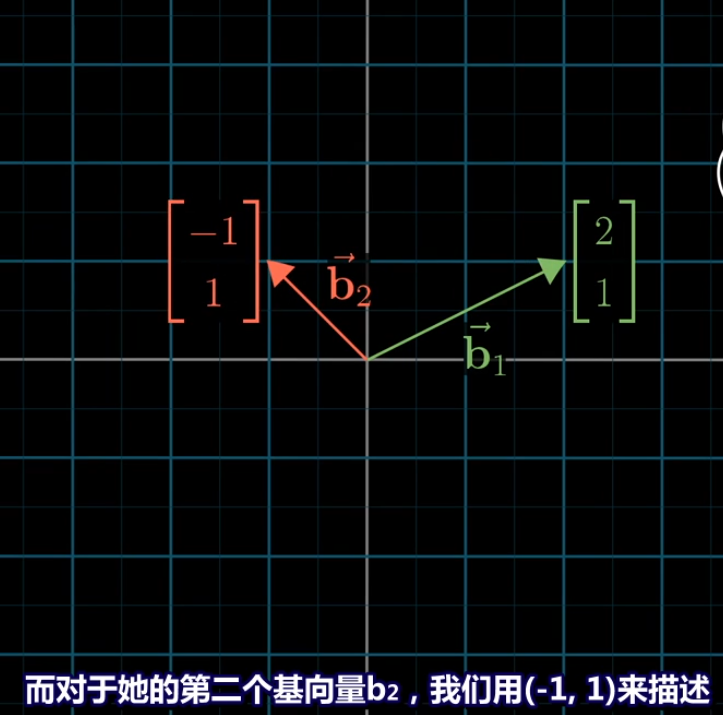
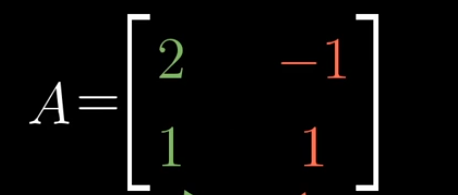

现在在原坐标系中有一个给定向量,知道坐标系B中基向量b1和b2在原坐标系坐标为(2,1)和(-1,1), 求给定向量在坐标系B中的坐标表示?
设给定向量在坐标系B中的表示为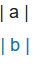 , 可知
在坐标系B中,a * b1 + b* b2 =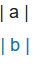。
那么 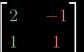* 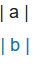 =  。
将在原坐标系中表示的b1和b2变为坐标系B中的基向量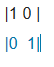。

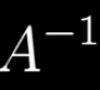 * 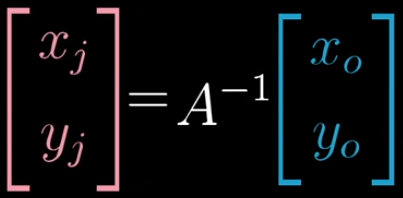
**所以**
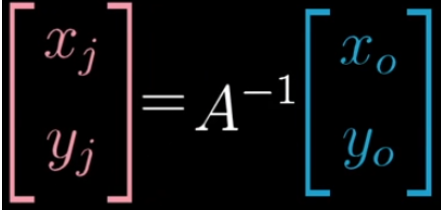
*****
将原坐标系上的一个线性变换M变为以A矩阵为基向量的B坐标系上的一个线性变换。
*****
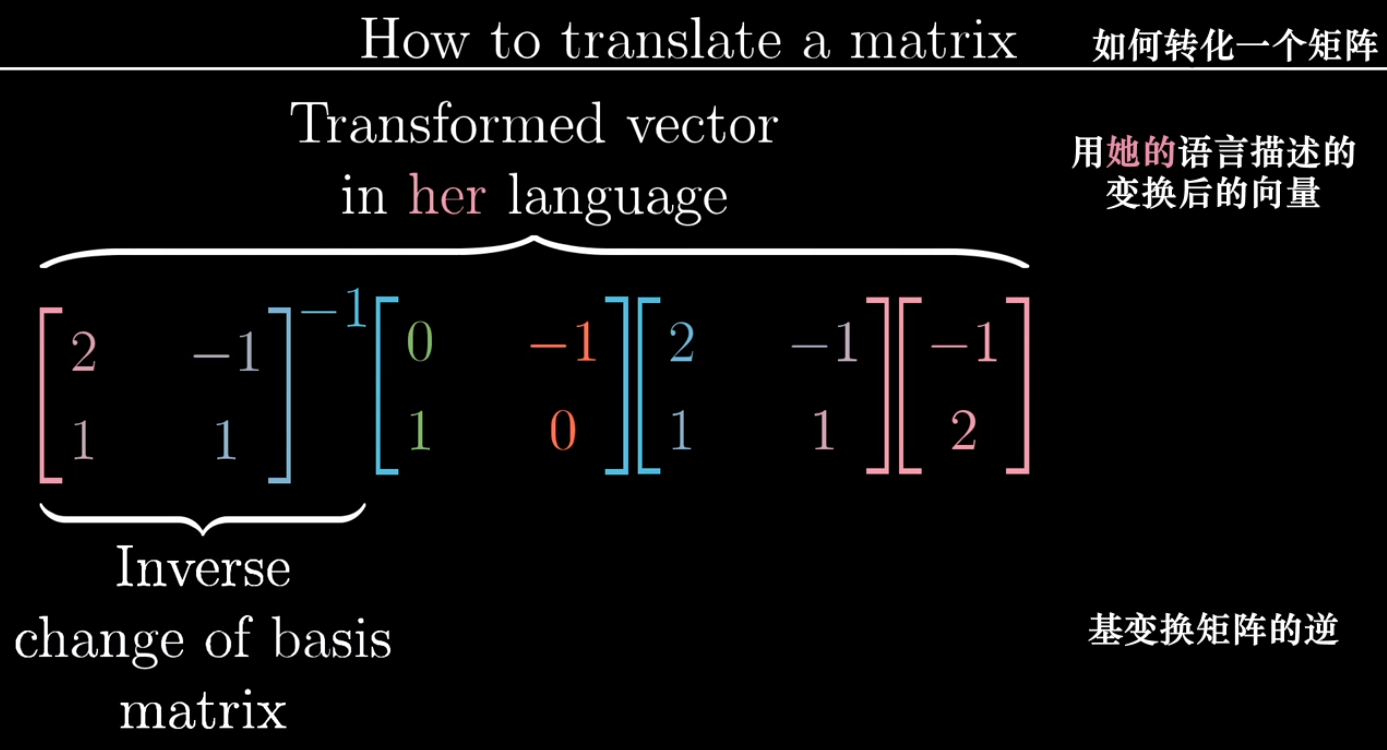
粉色是坐标系B上向量的坐标表示,蓝色用原坐标系表示线性变换。
从右往左,给定坐标系B上坐标表示向量v,和坐标系B上基向量的原坐标系坐标表示,再给一原坐标系上的线性变换,求线性变换后向量v在坐标系B上的坐标表示。
**求解过程:** 1. 先用基变换将向量v变为原坐标系上坐标表示的向量。2.再将该向量进行线性变换
3.将线性变换的结果进行基变换的逆变换,得到向量v线性变换后在坐标系B上的坐标表示
*****


